Question Corner and Discussion Area
Question Corner and Discussion Area
My name is Krishna. I'm now in Grade 12. When I was in Grade 11, I saw a question in the math club.The reason an infinite sum like 1 + 1/2 + 1/4 + · · · can have a definite value is that one is really looking at the sequence of numbersActually, I have already asked a similar question like the one below, but this one is little different.
The question is,
What is the value of, 1 + (1/2) + (1/4) + (1/8) ...... ?
How can you find a definite value for an answer when it keeps on continuing?
Thank you.
Krishna
1etc.,
1 + 1/2 = 3/2
1 + 1/2 + 1/4 = 7/4
1 + 1/2 + 1/4 + 1/8 = 15/8
and this sequence of numbers (1, 3/2, 7/4, 15/8, . . . ) is converging to a limit. It is this limit which we call the "value" of the infinite sum.
How do we find this value?
If we assume it exists and just want to find what it is, let's call it S. Now
S = 1 + 1/2 + 1/4 + 1/8 + · · ·so, if we multiply it by 1/2, we get
(1/2) S = 1/2 + 1/4 + 1/8 + 1/16 + · · ·Now, if we subtract the second equation from the first, the 1/2, 1/4, 1/8, etc. all cancel, and we get S - (1/2)S = 1 which means S/2 = 1 and so S = 2.
This same technique can be used to find the sum of any "geometric series", that it, a series where each term is some number r times the previous term. If the first term is a, then the series is
S = a + a r + a r^2 + a r^3 + · · ·so, multiplying both sides by r,
r S = a r + a r^2 + a r^3 + a r^4 + · · ·and, subtracting the second equation from the first, you get S - r S = a which you can solve to get S = a/(1-r). Your example was the case a = 1, r = 1/2.
In using this technique, we have assumed that the infinite sum exists, then found the value. But we can also use it to tell whether the sum exists or not: if you look at the finite sum
S = a + a r + a r^2 + a r^3 + · · · + a r^nthen multiply by r to get
rS = a r + a r^2 + a r^3 + a r^4 + · · · + a r^(n+1)and subtract the second from the first, the terms a r, a r^2, . . . , a r^n all cancel and you are left with S - r S = a - a r^(n+1), so
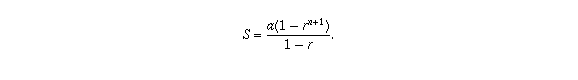
As long as |r| < 1, the term r^(n+1) will go to zero as n goes to infinity, so the finite sum S will approach a / (1-r) as n goes to infinity. Thus the value of the infinite sum is a / (1-r), and this also proves that the infinite sum exists, as long as |r| < 1.
In your example, the finite sums were
1 = 2 - 1/1and so on; the nth finite sum is 2 - 1/2^n. This converges to 2 as n goes to infinity, so 2 is the value of the infinite sum.
3/2 = 2 - 1/2
7/4 = 2 - 1/4
15/8 = 2 - 1/8
![]() Go backward to Finding the Sum of a Power Series
Go backward to Finding the Sum of a Power Series![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to A Complicated-Looking Infinite Sum
Go forward to A Complicated-Looking Infinite Sum![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page