Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE) (These buttons explained below)
UNIVERSITY OF TORONTO MATHEMATICS NETWORK

Question Corner and Discussion Area

A Complicated-Looking Infinite Sum

Asked by Andrew Gill, student, State College Area High School on August 8, 1997:
I have been trying to find the sum of:

(IMAGE)

(where n is a positive integer), but have not been able to find the process for evaluating this power series. Any and all information on this problem would be greatly appreciated.

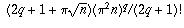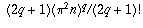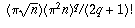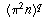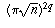This summation can be broken up and rewritten. Splitting the fraction into two pieces by writing (IMAGE) as the sum of (IMAGE) and (IMAGE) , then rewriting (IMAGE) as (IMAGE) and simplifying, gives

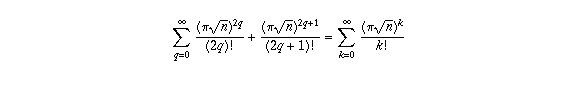
(IMAGE)

(the first sum runs over all even integers k=2q, the second over all odd integers k=2q+1, so the combined sum runs over all integers k).

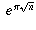Now you should notice that the last summation is just the power series expansion of (IMAGE) .

[ Submit Your Own Question ] [ Create a Discussion Topic ]
This part of the site maintained by (No Current Maintainers)
Last updated: April 19, 1999
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Current Network Coordinator and Contact Person: Joel Chan - mathnet@math.toronto.edu

Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE)

(IMAGE) Go backward to The Sum of the Geometric Series 1 + 1/2 + 1/4 + ...
(IMAGE) Go up to Question Corner Index
(IMAGE) Go forward to A Geometric Series Arising From an Arithmetic Series
(SWITCH TO TEXT-ONLY VERSION) Switch to text-only version (no graphics)
(IMAGE) Access printed version in PostScript format (requires PostScript printer)
(IMAGE) Go to University of Toronto Mathematics Network Home Page