Question Corner and Discussion Area

The n=4 Case of Fermat's Last Theorem

I want to prove, using mathematical induction, that there are no solutions to the equation , for positive values of x, y, z.

Those reading this page will likely recognize this question as the n=4 case of Fermat's Last Theorem. The general theorem (that, when n > 2, there are no positive integer solutions to the equation 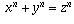), was conjectured by Fermat hundreds of years ago but remained unproved until just recently, when it was proved by Andrew Wiles. The proof is highly complex and involves some deep areas of abstract mathematics.

The n=4 case, however, is relatively easy to prove and was known by Fermat. It turns out to be a little easier to prove the more general result that there is no solution in positive integers to the equation 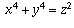(that is, the sum of two fourth powers cannot even be a perfect square, let alone a fourth power).

This is traditionally proven using the "method of infinite descent". The key to this method is the key lemma below (I'll explain later how this fact is proven).

Key Lemma. If 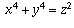where x, y, and z are positive integers, then there would exist other positive integers u, v, and w with 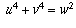, and w < z.

(For those unfamiliar with the terminology: a lemma is a small theorem whose main use is in proving another, more important, theorem).

The reason this lemma implies that solutions cannot exist is as follows. Suppose solutions did exist. Among all solutions, pick one with the smallest z value (any nonempty set of postive integers has a smallest element). But now the lemma says there would be another solution with a still smaller z value, a contradiction. Therefore, solutions cannot exist.

You can phrase this using the language of mathematical induction, but it's more awkward. You would work by induction on z. When z=1 there are clearly no solutions (x and y have to be at least 1, so 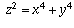has to be at least 2).

Now, if it is known that there are no solutions with 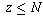, you can prove that there are no solutions with z=N+1 either: if (x,y,z) were such a solution, then the lemma implies that there is another solution (u,v,w) with w < z, so 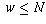, contradicting the fact that we know no such solution exists.

The above two paragraphs form the basis and induction steps for a proof by induction. But it's a little cleaner to use the method of infinite descent.

Now for the hard part: a proof of the lemma. I won't fill in all the details (since you originally posted this in the Discussion Topics section rather than the Questions section, I assume you don't want me too), but I will outline the proof.

It depends on the theory of Pythagorean triples. A triple (a,b,c) of positive integers is called a Pythagorean triple if 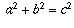. It is called a fundamental Pythagorean triple if a, b, and c have no common factor greater than 1.

For any fundamental Pythagorean triple, one of a and b is even and the other is odd. Let's use the letter a to refer to the even one, b to the odd one. Then there are positive integers m and n such that

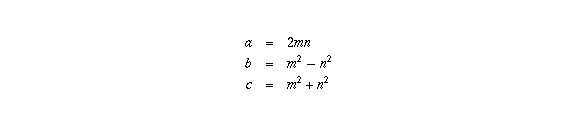
and m and n are relatively prime (have no common factor greater than 1).

If you don't know how to prove the above statements, feel free to post another question here.

Now, suppose 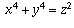. Then 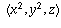is a Pythagorean triple.

If x, y, and z have a common prime factor p > 1, then 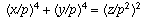and we have our desired solution (u,v,w) with u = x/p, v = y/p, and 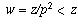. (You need also to explain why 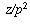is an integer; I'll leave that to you).

On the other hand, if x, y, and z do not have a common prime factor, then 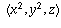is a fundamental Pythagorean triple. One of x and y is even and the other odd; let's use x to denote the even one. Then, by the theory of Pythagorean triples, there are relatively prime positive integers m and n such that

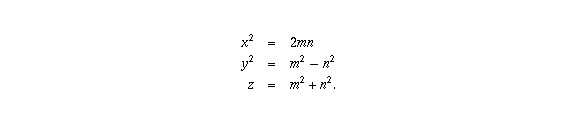
We can rewrite the second equation as 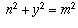. We know that m and n have no common factor greater than 1, so (n,y,m) is a fundamental Pythagorean triple. We know y is odd, so n must be the even one. Therefore, appealing to the theory of Pythagorean triples once again, there are relatively prime positive integers r and s such that

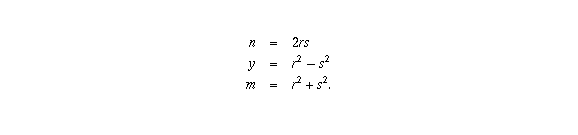
The final piece of the puzzle is the fact that if the product of two relatively prime positive integers is a perfect square, then each individually is a perfect square. From this it follows that m and n/2 are perfect squares, since the product is 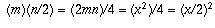(remember that x and n are even, so x/2 and n/2 are integers).

It also follows that r and s are perfect squares, since the product is 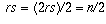which is a perfect square.

Therefore, setting 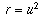, , 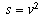, 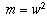the equation 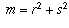becomes 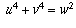. All that remains to complete the proof of the lemma is to show that w < z, which follows because 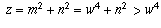, so 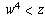, and as w is a positive integer this implies w < z as well.

If you want proofs of some of the statements I've left for you to fill in, just post a message here and we'd be glad to fill them in for you.

Go backward to Published Proof of Fermat's Last Theorem
Go up to Question Corner Index
Go forward to The Case n=3 Of Fermat's Last Theorem
Switch to text-only version (no graphics)
Access printed version in PostScript format (requires PostScript printer)
Go to University of Toronto Mathematics Network Home Page