These homework problems are meant to expand your understanding of what
goes on during class. Any you turn in will be graded and returned to
you. Answers may or may not be posted on the web, depending on demand.
- Construct a tetrahedron (if you haven't already) and find the number
of order-preserving symmetries of this polyhedron. In class it was
suggested that the order of this tetrahedral group
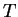 (that
is, the number of elements of
(that
is, the number of elements of 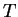 ) is
) is 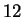 . Prove this by
. Prove this by
(a) showing that there are at least 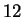 symmetries, and
symmetries, and
(b) showing that there are at most 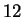 symmetries.
symmetries.
This is called a combinatorial (or counting) argument.
- In class we showed that the cube and octehedron shared an
orientation-preserving symmetry group (called
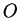 , the
octahedral group) as did the dodecahedron and the icosahedron
(this is
, the
octahedral group) as did the dodecahedron and the icosahedron
(this is 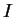 , the icosahedral group). People made the
following conjectures:
, the icosahedral group). People made the
following conjectures:
Hamoon's second conjecture:
The order of each of these symmetry groups is twice the number of
edges.
Martin's conjecture:
The order of each of these symmetry groups is the number of faces
times the number of edges per face.
Both of these conjectures result in the following orders: 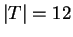 ,
,
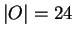 , and
, and 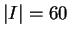 . Prove either of these conjectures, or at
least explain why you believe one of them.
. Prove either of these conjectures, or at
least explain why you believe one of them.
- A group
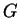 is called abelian (or commutative) if
is called abelian (or commutative) if 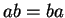 for all elements
for all elements 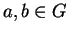 . Prove that
. Prove that 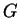 is abelian if and
only if
is abelian if and
only if
(a)
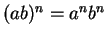 for all elements
for all elements 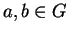 and for all
positive integers
and for all
positive integers 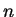
(b)
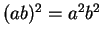 for all elements
for all elements 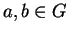
(c)
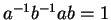 for all elements
for all elements 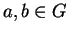
(d)
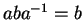 for all elements
for all elements
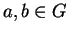
(e)
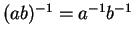 for all elements
for all elements 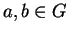
(f)
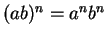 for all elements
for all elements 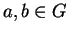 and for all
negative integers
and for all
negative integers 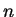
(g) (Harder!)
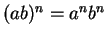 for all elements
for all elements 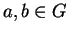 for
for 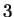 consecutive integers
consecutive integers 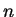 .
.
- (Still difficult!)
Give an example to show that part (g) of the previous problem
would not be true if we only had the property for
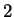 consecutive
integers
consecutive
integers 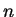 .
.
-
A group
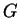 is called cyclic if there is an element
is called cyclic if there is an element 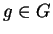 so
that any element
so
that any element 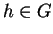 may be written as
may be written as 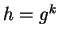 for some
positive integer
for some
positive integer 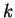 . The element
. The element 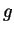 is called the generator
of
is called the generator
of 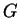 .
.
Prove that every cyclic group is abelian.
- Let
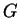 be a group of order
be a group of order 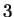 . Prove that
. Prove that 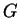 is cyclic (and
therefore abelian). Does your proof still work if
is cyclic (and
therefore abelian). Does your proof still work if 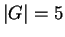 ? Can you
make a generalization of this statement (and proof)?
? Can you
make a generalization of this statement (and proof)?
- Let
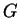 be any finite group (this means that
be any finite group (this means that 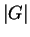 is finite), and let
is finite), and let
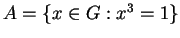 . Prove that
. Prove that
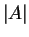 is
odd.
is
odd.
- This one gets a little challenging towards the end.
(a) Prove that if 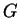 is a group of even order then
is a group of even order then 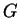 has an
element of order
has an
element of order 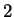 .
.
(b) We now know that if 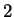 divides
divides
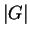 , then
, then 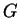 has
an element of order
has
an element of order 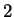 . Prove that if
. Prove that if 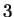 divides
divides
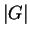 , then
, then 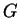 has an element of order
has an element of order 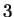 .
.
(c) Can you state a generalization of this result?
(d) Prove your generalization.
These problems are also available as a ![]() symmetries, and
symmetries, and
![]() symmetries.
symmetries.
![]() ,
,
![]() , and
, and ![]() . Prove either of these conjectures, or at
least explain why you believe one of them.
. Prove either of these conjectures, or at
least explain why you believe one of them.
![]() for all elements
for all elements ![]() and for all
positive integers
and for all
positive integers ![]()
![]() for all elements
for all elements ![]()
![]() for all elements
for all elements ![]()
![]() for all elements
for all elements
![]()
![]() for all elements
for all elements ![]()
![]() for all elements
for all elements ![]() and for all
negative integers
and for all
negative integers ![]()
![]() for all elements
for all elements ![]() for
for ![]() consecutive integers
consecutive integers ![]() .
.
![]() is a group of even order then
is a group of even order then ![]() has an
element of order
has an
element of order ![]() .
.
![]() divides
divides
![]() , then
, then ![]() has
an element of order
has
an element of order ![]() . Prove that if
. Prove that if ![]() divides
divides
![]() , then
, then ![]() has an element of order
has an element of order ![]() .
.