Solution of Term Exam 1
Problem 1. Find formulas for
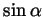 ,
,
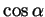 and
and
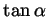 in terms of
in terms of
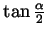 . (You may use any
formula proven in class; you need to quote such formulae, though you
don't need to reprove them).
. (You may use any
formula proven in class; you need to quote such formulae, though you
don't need to reprove them).
Solution. (Graded by Shay Fuchs) Using the formulas
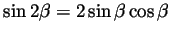 and
and
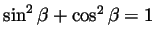 and taking
and taking
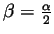 we get
we get
Dividing the numerator and denominator by
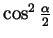 this
becomes
Likewise using
this
becomes
Likewise using
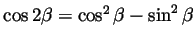 we get
Finally, dividing these two formulas by each other we get
we get
Finally, dividing these two formulas by each other we get
Problem 2.
- Let
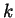 be a natural number. Prove that any
natural number
be a natural number. Prove that any
natural number 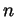 can be written in a unique way in the form
can be written in a unique way in the form 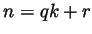 ,
where
,
where 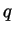 and
and 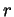 are integers and
are integers and 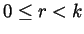 .
.
- We say that a natural number
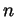 is ``divisible by
is ``divisible by 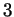 '' if
'' if 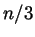 is
again a natural number. Prove that
is
again a natural number. Prove that 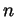 is divisible by
is divisible by 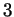 if and only if
if and only if
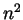 is divisible by
is divisible by 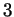 .
.
- We say that a natural number
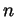 is ``divisible by
is ``divisible by 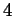 '' if
'' if 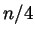 is
again a natural number. Is it true that
is
again a natural number. Is it true that 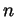 is divisible by
is divisible by 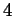 if and only
if
if and only
if 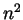 is divisible by
is divisible by 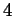 ?
?
Solution. (Graded by Brian Pigott)
- We prove this assertion (without uniqueness) by induction. If
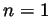 write
write 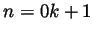 (if
(if 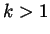 ) or
) or 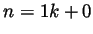 (if
(if 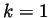 ). In either case
the assertion is proven for
). In either case
the assertion is proven for 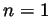 . Now assume
. Now assume 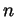 can be written in the
form
can be written in the
form 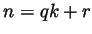 , where
, where 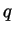 and
and 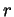 are integers and
are integers and 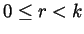 . If
. If
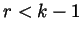 then
then 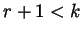 and so
and so
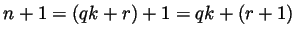 is a formula of the
desired form for
is a formula of the
desired form for 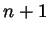 . Otherwise
. Otherwise 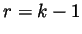 and so
and so
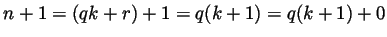 , and again that's a formula of the
desired form for
, and again that's a formula of the
desired form for 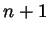 . This concludes the proof that every natural
number
. This concludes the proof that every natural
number 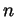 can be written in the form
can be written in the form 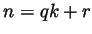 , where
, where 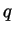 and
and 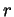 are
integers and
are
integers and 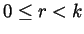 . Now assume it can be done in two ways; i.e.,
assume
. Now assume it can be done in two ways; i.e.,
assume
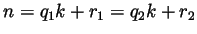 where
where 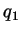 ,
, 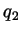 ,
, 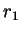 and
and 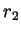 are
integers and
are
integers and
 . But then
. But then
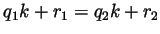 and so
and so
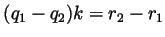 and so
and so
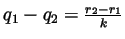 . But
. But 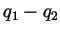 is an integer and so
is an integer and so
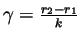 is an integer. From
is an integer. From
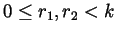 it follows that
it follows that
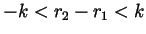 and so
and so
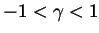 and so the integer
and so the integer 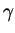 must be 0. Thus
must be 0. Thus
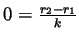 and
so
and
so 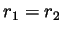 . But then the equality
. But then the equality
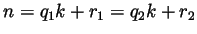 implies
implies
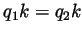 and so
and so 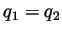 and we see that the pair
and we see that the pair 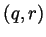 is
unique.
is
unique.
- An integer
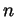 is divisible by
is divisible by 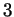 iff
iff 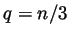 is an integer iff
is an integer iff
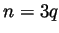 with an integer
with an integer 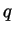 . Now if
. Now if 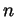 is divisible by
is divisible by 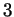 then
then 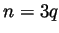 with an integer
with an integer 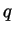 and then
and then
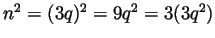 . So
. So 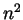 is
also
is
also 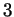 times an integer (the integer
times an integer (the integer 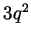 ), and so
), and so 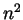 is also
divisible by
is also
divisible by 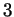 . Assume now that
. Assume now that 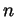 is not divisible by
is not divisible by 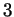 . By the
previous part
. By the
previous part 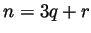 with integer
with integer 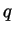 and
and 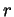 and with
and with 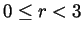 .
Had
.
Had 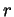 been 0 we'd have had that
been 0 we'd have had that 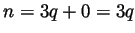 is divisible by
is divisible by 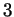 contrary to assumption. So
contrary to assumption. So 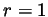 or
or 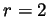 . In the former case
. In the former case
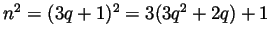 , but then by the uniqueness of writing
, but then by the uniqueness of writing
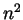 as
as 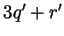 it follows that
it follows that 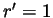 , so
, so 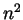 cannot be written in
the form
cannot be written in
the form 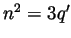 , so
, so 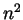 is not divisible by
is not divisible by 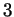 . In the latter
case
. In the latter
case
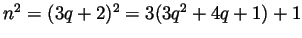 and for the same reason again we
find that
and for the same reason again we
find that 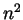 is not divisible by
is not divisible by 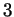 . So if
. So if 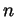 is divisible by
is divisible by 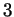 so is
so is 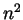 , and if
, and if 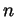 is not divisible by
is not divisible by 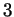 so is
so is 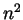 .
.
- No it's not true. Example:
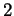 is not divisible by
is not divisible by 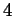 but
but 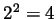 is divisible by
is divisible by 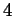 .
.
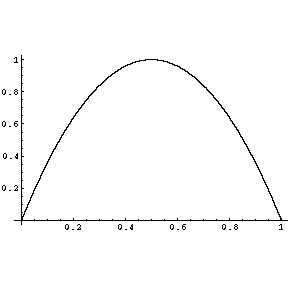
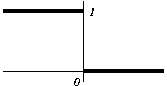
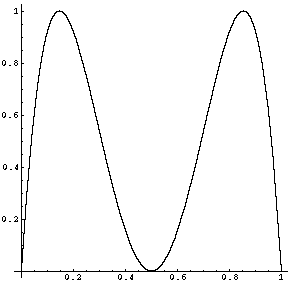
Problem 3. A function 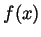 is defined for
is defined for
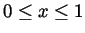 and has the graph plotted above.
and has the graph plotted above.
- What are
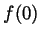 ,
, 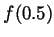 and
and 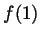 ?
?
- Let
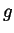 be the function
be the function 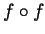 . What are
. What are 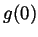 ,
, 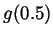 and
and
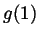 ?
?
- Are there any values of
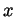 for which
for which 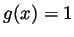 ? How many
such
? How many
such 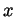 's are there? Roughly what are they?
's are there? Roughly what are they?
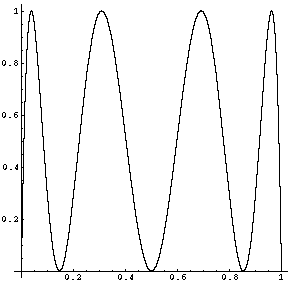
- Plot the graph of the function
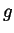 . (The general shape of your plot
should be clear and correct, though numerical details need not be precise).
. (The general shape of your plot
should be clear and correct, though numerical details need not be precise).
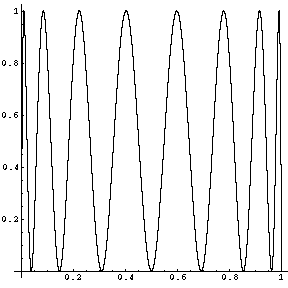
- (5 points bonus, will be given only to excellent solutions and
may raise your overall exam grade to 105!) Plot the graphs of the
functions
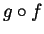 and
and 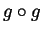 .
.
Solution. (Graded by Derek Krepski)
- By inspecting the graph,
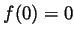 ,
, 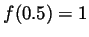 and
and 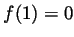 .
.
-
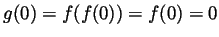 ,
,
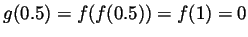 and
and
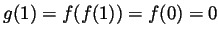 .
.
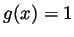 means
means 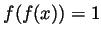 . Denoting
. Denoting 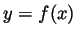 we must have
we must have 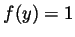 ,
and inspecting the graph we find that
,
and inspecting the graph we find that 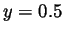 . Thus
. Thus 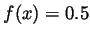 . Inspecting
the graph we find that there are two values of
. Inspecting
the graph we find that there are two values of 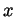 for which this happens
and they are approximately
for which this happens
and they are approximately 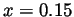 and
and 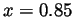 .
.
- and 5.:
Problem 4.
- Define ``
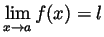 '' and ``
'' and ``
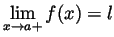 ''.
''.
- Prove that if
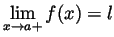 and
and
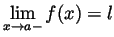 then
then
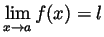 .
.
- Prove that if
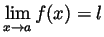 then
then
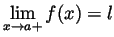 and
and
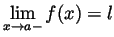 .
.
- Draw the graph of some function for which
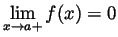 and
and
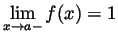 .
.
Solution. (Graded by Shay Fuchs)
- ``
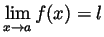 '' means that for every
'' means that for every
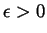 there is a
there is a 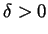 so that whenever
so that whenever
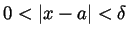 we have that
we have that
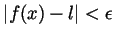 , while ``
, while ``
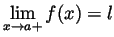 '' means that for
every
'' means that for
every
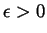 there is a
there is a 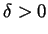 so that whenever
so that whenever
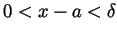 (i.e., whenever
(i.e., whenever
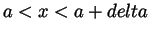 ) we have that
) we have that
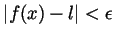
- Let
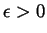 be given. Using
be given. Using
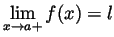 choose
choose
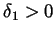 so that whenever
so that whenever
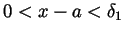 we have that
we have that
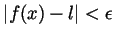 . Using
. Using
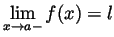 choose
choose
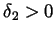 so that whenever
so that whenever
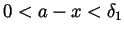 we have that
we have that
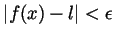 . Set
. Set
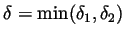 and assume
and assume
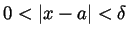 . If
. If 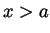 then
then
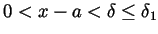 and by the
choice of
and by the
choice of 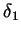 it follows that
it follows that
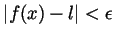 . If
. If 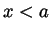 then
then
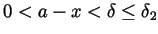 and by the choice of
and by the choice of 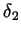 it follows
that
it follows
that
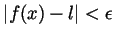 . So in any case,
. So in any case,
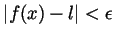 as
required.
as
required.
- Let
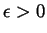 be given. Using
be given. Using
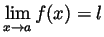 choose
choose
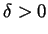 so that whenever
so that whenever
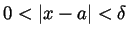 we have that
we have that
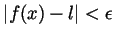 .
But then if
.
But then if
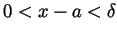 then certainly
then certainly
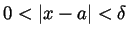 so by the choice
of
so by the choice
of 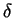 we get
we get
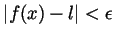 . Thus
. Thus
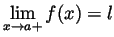 . A
similar argument shows that also
. A
similar argument shows that also
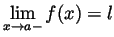 .
.
-
Problem 5. Give examples to show that the
following definitions of
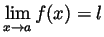 do not
agree with the standard one:
do not
agree with the standard one:
- For all
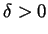 there is an
there is an
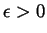 such that if
such that if
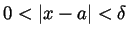 , then
, then
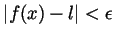 .
.
- For all
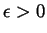 there is a
there is a 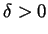 such that if
such that if
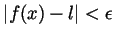 , then
, then
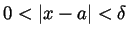 .
.
Solution. (Graded by Derek Krepski)
- This is satisfied whenever there exists a constant
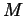 so that
so that
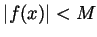 for all
for all 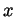 and regardless of the limit of
and regardless of the limit of 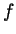 . Indeed,
choose
. Indeed,
choose 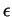 bigger than
bigger than 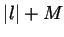 where
where 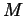 is a constant as in the
previous sentence (for example, if
is a constant as in the
previous sentence (for example, if 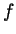 is
is 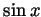 , then
, then 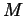 can be
chosen to be
can be
chosen to be 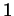 ), and then
), and then
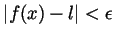 is always true.
is always true.
- According to this definition, for example,
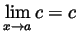 is false, and hence it cannot be equivalent to the standard
definition. Indeed, in this case
is false, and hence it cannot be equivalent to the standard
definition. Indeed, in this case
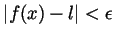 means
means
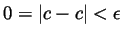 .
This imposes no condition on
.
This imposes no condition on 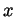 , so
, so 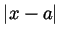 need not be smaller than
need not be smaller than
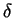 .
.
The results. 89 students took the exam; the average
grade was 59 and the standard deviation was about 18.5.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2004-10-20
![]() ,
,
![]() and
and
![]() in terms of
in terms of
![]() . (You may use any
formula proven in class; you need to quote such formulae, though you
don't need to reprove them).
. (You may use any
formula proven in class; you need to quote such formulae, though you
don't need to reprove them).
![]() and
and
![]() and taking
and taking
![]() we get
we get
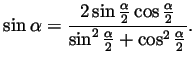
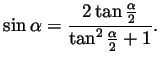
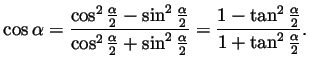
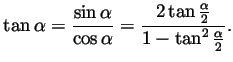

![]() is defined for
is defined for
![]() and has the graph plotted above.
and has the graph plotted above.

![]() do not
agree with the standard one:
do not
agree with the standard one: