


Next: 3.2 Preliminaries
Up: 3. The case of
Previous: 3. The case of
Definition 3.1
An
n-singular integral homology sphere is a pair
(
M,
L) where
M is an integral homology sphere and
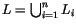
is a unit-framed algebraically split ordered
n-component link
in
M. Namely, the components
Li of
M are numbered 1 to
n(``ordered''), framed with
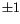
framing (``unit framed''), and the
pairwise linking numbers between the different components of
L are
0 (``algebraically split''). We think of
L as marking
n sites for
performing small modifications of
M, each modification being the surgery
on one of the components of
L. Let us temporarily define
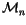
to be the

-module of all formal

-linear combinations of
n-singular integral homology spheres. A correction to the definition of
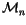
will be given in Definition
3.2 below. Notice that
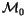
,
which we often simply denote by
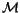
,
is simply the space of
all

-linear combinations of integral homology spheres.
If
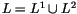 is a framed link (presented as a union of two sublinks
L1 and L2) in some 3-manifold M, we denote by
(M,L1)L2the result of surgery2
of (M,L1) along L2. Namely,
(M,L1)L2 is a pair
(M',L1'),
in which M' is the result of surgery of M along L2, and L1'is the image in M' of L1. Notice that if (M,L) is an
(n+1)-singular integral homology sphere, then
(M,L-Li)Li is again
an n-singular integral homology sphere for any component Li of L.
is a framed link (presented as a union of two sublinks
L1 and L2) in some 3-manifold M, we denote by
(M,L1)L2the result of surgery2
of (M,L1) along L2. Namely,
(M,L1)L2 is a pair
(M',L1'),
in which M' is the result of surgery of M along L2, and L1'is the image in M' of L1. Notice that if (M,L) is an
(n+1)-singular integral homology sphere, then
(M,L-Li)Li is again
an n-singular integral homology sphere for any component Li of L.
We now wish to define the co-derivative map
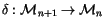 ,
whose adjoint will be the differentiation map for invariants:
,
whose adjoint will be the differentiation map for invariants:
Definition 3.2
Define
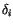
on generators by
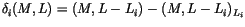
,
and extend it to be a

-linear map
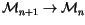
.
For later convinience, we
want to set
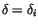
for any
i, but the different
i's may
give different answers. We resolve this by redefining
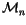
.
Set
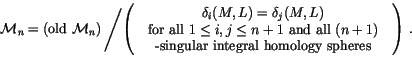 |
(5) |
We can now set (in the new
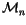
)
The relations in equation (
5) are called ``the
co-differentiability relations''.
We can finally differentiate invariants using the adjoint
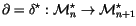 .
That is,
if
.
That is,
if
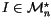 is a differentiable invariant of n-singular
integral homology spheres (namely, which vanishes on the
co-differentiability relations), let its derivative
is a differentiable invariant of n-singular
integral homology spheres (namely, which vanishes on the
co-differentiability relations), let its derivative
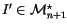 be
be
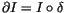 .
Iteratively, one can define multiple
derivatives such us I(k) for any
.
Iteratively, one can define multiple
derivatives such us I(k) for any 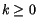 .
.
Definition 3.3
(Ohtsuki [
Oh1]
We say that an invariant
I of integral homology spheres is of type
nif its
n+1st derivative vanishes. We say that it is of finite type if it
is of type
n for some natural number
n.
Unravelling the definitions, we find that I is of type n precisely when
for all integral homology spheres M and all unit-framed algebraically
split (n+1)-component links L in M,
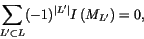 |
(6) |
where the sum runs on all sublinks L' of L (including the empty and
full sublinks), |L'| is the number of components of L', and ML' is
the result of surgery of M along L'. We will not use
equation (6) in this paper.
Footnotes
- ... surgery2
-
We recall some basic facts about surgery in
Section 3.2.1.



Next: 3.2 Preliminaries
Up: 3. The case of
Previous: 3. The case of
Dror Bar-Natan
2000-03-19
![]() is a framed link (presented as a union of two sublinks
L1 and L2) in some 3-manifold M, we denote by
(M,L1)L2the result of surgery2
of (M,L1) along L2. Namely,
(M,L1)L2 is a pair
(M',L1'),
in which M' is the result of surgery of M along L2, and L1'is the image in M' of L1. Notice that if (M,L) is an
(n+1)-singular integral homology sphere, then
(M,L-Li)Li is again
an n-singular integral homology sphere for any component Li of L.
is a framed link (presented as a union of two sublinks
L1 and L2) in some 3-manifold M, we denote by
(M,L1)L2the result of surgery2
of (M,L1) along L2. Namely,
(M,L1)L2 is a pair
(M',L1'),
in which M' is the result of surgery of M along L2, and L1'is the image in M' of L1. Notice that if (M,L) is an
(n+1)-singular integral homology sphere, then
(M,L-Li)Li is again
an n-singular integral homology sphere for any component Li of L.
![]() ,
whose adjoint will be the differentiation map for invariants:
,
whose adjoint will be the differentiation map for invariants:
![]() .
That is,
if
.
That is,
if
![]() is a differentiable invariant of n-singular
integral homology spheres (namely, which vanishes on the
co-differentiability relations), let its derivative
is a differentiable invariant of n-singular
integral homology spheres (namely, which vanishes on the
co-differentiability relations), let its derivative
![]() be
be
![]() .
Iteratively, one can define multiple
derivatives such us I(k) for any
.
Iteratively, one can define multiple
derivatives such us I(k) for any ![]() .
.