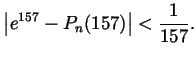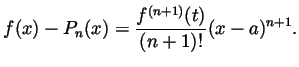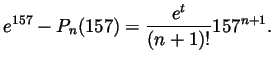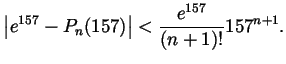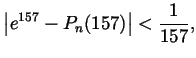Solution of Term Exam 4
Problem 1. Agents of
CSIS have secretly developed a
function 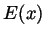 that has the following properties:
that has the following properties:
-
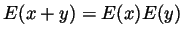 for all
for all
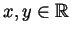 .
.
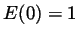
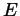 is differentiable at 0 and
is differentiable at 0 and 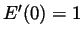 .
.
Prove the following:
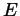 is everywhere differentiable and
is everywhere differentiable and 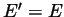 .
.
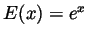 for all
for all
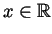 . The only lemma you may assume is that
if a function
. The only lemma you may assume is that
if a function 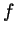 satisfies
satisfies 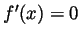 for all
for all 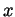 then
then 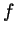 is a constant
function.
is a constant
function.
Solution. (Graded by Brian Pigott)
- The fact that
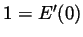 means that
means that
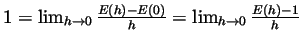 . Hence,
using
. Hence,
using
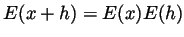 we get
This proves both that
we get
This proves both that 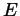 is differentiable at
is differentiable at 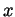 and that
and that
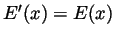 .
.
- Consider
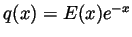 . Differentiating we get
Hence
. Differentiating we get
Hence 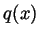 is a constant function. But
is a constant function. But
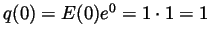 , hence
this constant must be
, hence
this constant must be 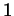 . So
. So
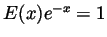 and thus
and thus 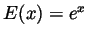 .
.
Problem 2. Compute the following integrals: (a few lines of
justification are expected in each case, not just the end result.)
-
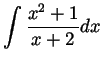 .
.
-
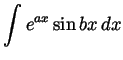 (assume that
(assume that
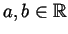 and that
and that
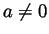 and
and 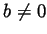 ).
).
-
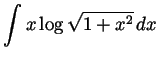 .
.
-
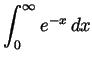 . (This, of course, is
. (This, of course, is
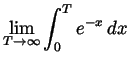 ).
).
Solution. (Graded by Shay Fuchs)
-
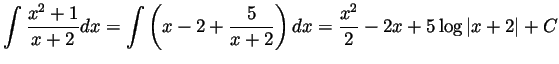 .
.
- Let
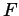 denote the anti-derivative we are interested in; i,e,,
denote the anti-derivative we are interested in; i,e,,
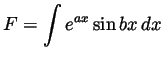 . Integrating by parts twice we get
. Integrating by parts twice we get
so
or
(with the 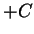 neglected).
neglected).
- Taking
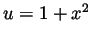 hence
hence 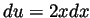 and using a formula from class,
and using a formula from class,
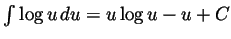 , we get
, we get
-
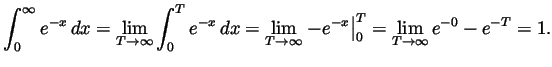
Problem 3.
- State (without proof) the formula for the surface area of an object
defined by spinning the graph of a function
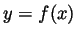 (for
(for
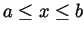 )
around the
)
around the  axis.
axis.
- Compute the surface area of a sphere of radius 1.
Solution. (Graded by Brian Pigott)
- That surface area, excluding the ``caps'', is
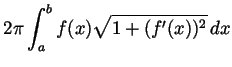 . Including the caps it is the
same plus the area of the caps,
. Including the caps it is the
same plus the area of the caps,
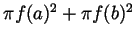 . For the purpose of
this exam, both solutions are acceptable.
. For the purpose of
this exam, both solutions are acceptable.
- Here
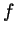 is the function whose graph is a semi-circle, so
is the function whose graph is a semi-circle, so
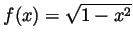 , and
, and 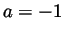 and
and 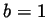 . By direct computation,
. By direct computation,
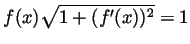 so the surface area of a sphere of radius 1 is
so the surface area of a sphere of radius 1 is
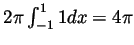 .
.
Problem 4.
- State and prove the remainder formula for Taylor polynomials (it is
sufficient to discuss just one form for the remainder, no need to mention
all the available forms).
- It is well known (and need not be reproven here) that the
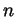 th
Taylor polynomial
th
Taylor polynomial
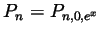 of
of 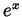 around 0 is given by
around 0 is given by
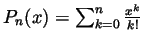 . It is also well known (and need not be
reproven here) that factorials grow faster than exponentials, so for any
fixed
. It is also well known (and need not be
reproven here) that factorials grow faster than exponentials, so for any
fixed 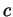 we have
we have
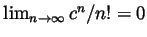 . Show that for large enough
. Show that for large enough 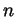 ,
,
Solution. (Graded by Derek Krepski)
- Statement: If
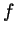 is differentiable
is differentiable 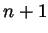 times on the interval
between
times on the interval
between 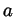 and
and 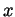 and if
and if 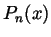 denotes the
denotes the 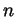 th Taylor polynomial of
th Taylor polynomial of
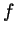 at
at 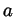 , then there is some
, then there is some 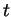 between
between 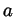 and
and 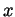 for which
Proof: See your class notes from March 10, 2005.
for which
Proof: See your class notes from March 10, 2005.
- By the remainder formula with
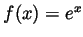 and with
and with 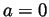 we have that
for any
we have that
for any 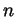 , there is a
, there is a
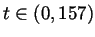 for which
But
for which
But 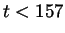 implies
implies
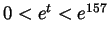 and so
Now take
and so
Now take 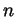 big enough so that
big enough so that
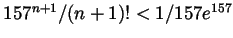 (this is
possible because
(this is
possible because
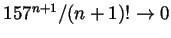 ) and get
as required.
) and get
as required.
The results. 66 students took the exam; the average
grade was 58.2 and the standard deviation was about 24.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2005-03-23
![]() that has the following properties:
that has the following properties:
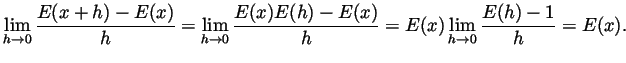
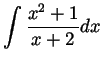 .
.
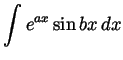 (assume that
(assume that
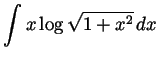 .
.
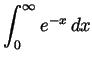 . (This, of course, is
. (This, of course, is
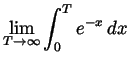 ).
).
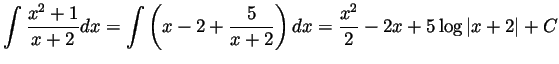 .
.
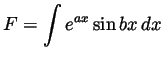 . Integrating by parts twice we get
. Integrating by parts twice we get
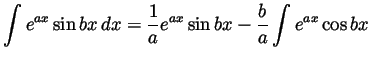
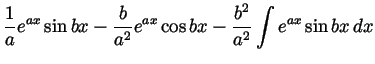
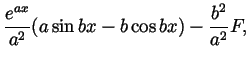
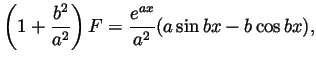
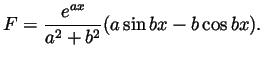
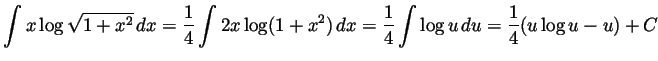
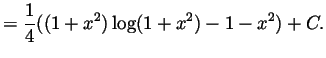
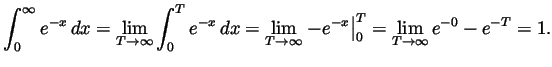
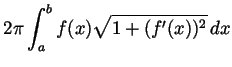 . Including the caps it is the
same plus the area of the caps,
. Including the caps it is the
same plus the area of the caps,