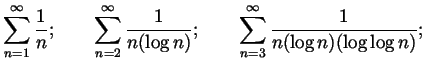
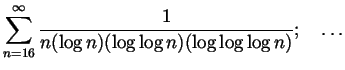
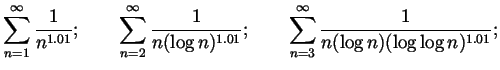
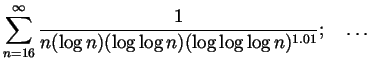
| © | Dror Bar-Natan: Classes: 2004-05: Math 157 - Analysis I: | (103) |
Next: Class Notes for Tuesday March 22, 2005
Previous: Solution of Term Exam 4 |
Required reading. All of Spivak's Chapters 22 and 23.
To be handed in. From Spivak Chapter 23: Problems 1 (parts divisible by 4), 12, 23.
Recommended for extra practice. From Spivak Chapter 23: Problems 1 (the rest), 5, 20, 21.
In class review problem(s) (to be solved in class on Thursday March 31):
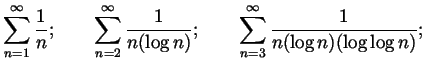
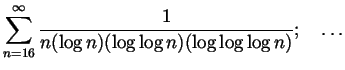
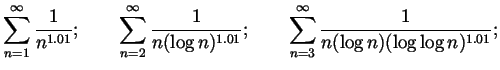
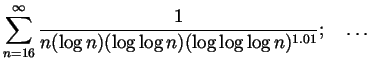
Just for fun.
In this question we always assume that ![]() and
and ![]() .
Let's say that a sequence
.
Let's say that a sequence ![]() is ``much bigger'' than a sequence
is ``much bigger'' than a sequence
![]() if
if
![]() . Likewise let's say that a
sequence
. Likewise let's say that a
sequence ![]() is ``much smaller'' than a sequence
is ``much smaller'' than a sequence ![]() if
if
![]() . Prove that for every convergent series
. Prove that for every convergent series
![]() there is a much bigger sequence
there is a much bigger sequence ![]() for which
for which ![]() is
also convergent, and that for every divergent series
is
also convergent, and that for every divergent series ![]() there is
a much smaller sequence
there is
a much smaller sequence ![]() for which
for which ![]() is also divergent. (Thus
you can forever search in vain for that fine line between good and evil; it
just isn't there).
is also divergent. (Thus
you can forever search in vain for that fine line between good and evil; it
just isn't there).
Advertisement 1'. A short addendum to Advertisement 1 of HW21:
Date: Sun, 20 Mar 2005 21:53:48 -0500 Dr. Bar-Natan: Thank you for posting our announcement on your website, the advertising is greatly appreciated! However, a minor note: technically, this event *does* include free food - 5 meals (not to mention a T-shirt!) are included in the $60 registration fee, truly a fantastic bargain! ;) Cheers, Erica Blom