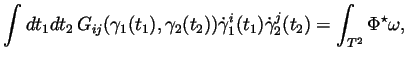The Final Exam
Solve and submit your solution of two (just two!) of the following
three questions by noon on Tuesday January 6, 2004. Remember -- Elegance counts!!! If you can type your solution, that's better. If
you can't, at least copy it again to a clean sheet of paper. Formulas
without words explaining them will not be accepted!
- Prove in detail:
- All torus knots, except for the obvious exceptions, are really
knotted.
- All knotted torus knots are prime.
- The ``Dubrovnik Polynomial''
 (a variant of the ``Kauffman
Polynomial''
(a variant of the ``Kauffman
Polynomial''  ) is an invariant of framed links valued in rational
functions in the variables
) is an invariant of framed links valued in rational
functions in the variables  and
and 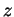 , satisfying the following
relations:
, satisfying the following
relations:
- Compute
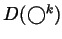 (where
(where
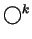 is the
is the 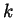 -component
unlink).
-component
unlink).
Hint. One instance of relation (4) relates
the following four knots; three of them are the unknot with different
framings:
- Prove that the above conditions determine
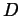 on all knots and links.
on all knots and links.
- Set
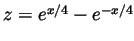 and
and
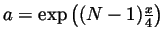 and expand
(here
and expand
(here 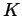 stands for an arbitrary knot or link). Prove that for any
stands for an arbitrary knot or link). Prove that for any
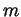 the coefficient
the coefficient 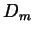 is a type
is a type 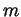 invariant of links with
values in polynomials in
invariant of links with
values in polynomials in 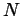 .
.
- Determine the weight system of
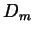 and show that it is the weight
system arising from the Lie algebra
and show that it is the weight
system arising from the Lie algebra 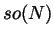 .
.
- Claim: The integral operator given by the kernel
is an inverse of the differential operator
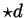 .
.
Explain what this claim means and prove it. This done, show that if
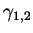 are disjoint space curves, then
are disjoint space curves, then
where
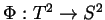 is the ``direction of sight'' map
is the ``direction of sight'' map
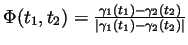 and
where
and
where 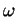 is the volume form of
is the volume form of 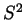 normalized so that the total
volume of
normalized so that the total
volume of 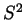 is
is 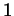 .
.
Good Luck!!
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2003-12-19
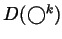 (where
(where
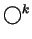 is the
is the 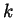 -component
unlink).
-component
unlink).
![$\displaystyle {\hspace{-3pt}\begin{array}{c}\raisebox{0mm}{\includegraphics[width=3in]{figs/FourKnots.eps}}\end{array}\hspace{-3pt}} $](img17.gif)
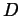 on all knots and links.
on all knots and links.
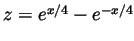 and
and
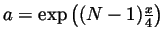 and expand
(here
and expand
(here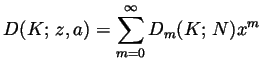
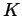 stands for an arbitrary knot or link). Prove that for any
stands for an arbitrary knot or link). Prove that for any
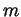 the coefficient
the coefficient 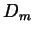 is a type
is a type 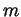 invariant of links with
values in polynomials in
invariant of links with
values in polynomials in 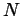 .
.
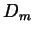 and show that it is the weight
system arising from the Lie algebra
and show that it is the weight
system arising from the Lie algebra 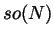 .
.
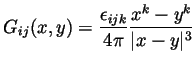
![]() are disjoint space curves, then
are disjoint space curves, then