Graphing
Worked Examples
Parabolas
A parabola is the graph of a quadratic polynomial in one variable (see more in the Polynomials section). Its general equation comes in three forms: \begin{array}{l l} \text{Standard form: } & y = ax^2 + bx + c \\ \text{Vertex form: } & y = a(x-h)^2 + k \\ \text{Factored form: } & y = a(x-r)(x-s) \end{array} The factored form of the equation tells us the roots, i.e. the $x$-intercepts, $x=r$ and $x=s$.The key information in drawing a parabola is the vertex, which we can read off from the vertex form equation as the point $(h,k)$.
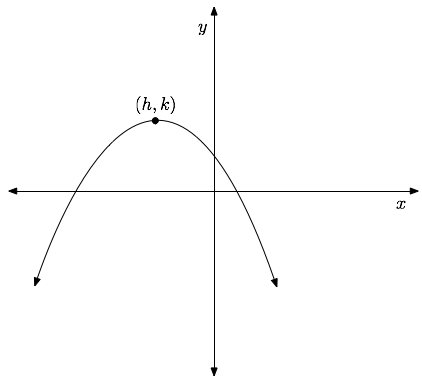
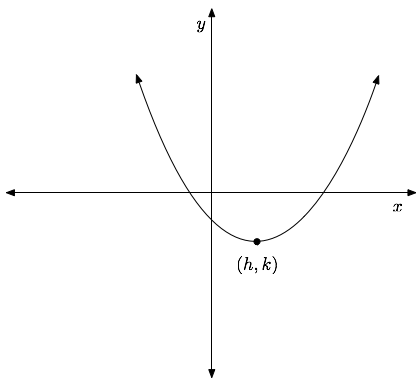
If $a>0$, the parabola opens upwards. Otherwise, for $a<0$, it opens downwards as illustrated below.
 |
 |
|
| A parabola in the case $a<0$ | A parabola in the case $a>0$ |
Note: For larger $|a|$, the graph will be narrower and for smaller $|a|$ the graph will be wider.
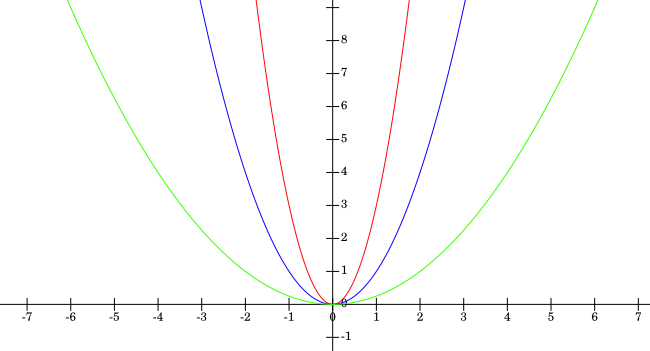
The graph of $y=ax^2$ illustrated for $a>1$ (red), $a=1$ (blue), and $0 < a < 1$ (green)
Drawing the parabola is easier if we have the vertex form of the equation, so we need to know how to go from the standard to the vertex form.
Completing the square
Going from the standard form to the vertex form of a quadratic equation involves "completing the square", as illustrated below: \begin{align*} y &= ax^2 + bx + c \\ y &= a\left(x^2 + \frac{b}{a}x\right) + c \\ y &= a\left(x^2+\frac{b}{a}x + \left(\frac{b}{2a}\right)^2 - \left(\frac{b}{2a}\right)^2 \right) + c \\ y &= a\left(x^2+\frac{b}{a}x + \frac{b^2}{4a^2}\right) - a \left(\frac{b^2}{4a^2}\right) + c \\ y &= a\left(x + \frac{b}{2a} \right)^2 - \left(\frac{b^2}{4a} - c \right) \\ y &= a\left(x + \frac{b}{2a} \right)^2 - \frac{b^2-4ac}{4a} \end{align*}Example. Draw the parabola with equation $y = 3x^2 + 12x + 8$.
Solution: Completing the square, we get that the vertex form of the equation of this parabola is: $$y = 3(x + 2)^2 - 4$$ So, the vertex of this parabola is $(-2,-4)$.It intersects the $y$-axis when $x=0$, then we get $y = 3(2)^2-4=8$. It intersects the $x$-axis when $y=0$, then $0 = 3(x+2)^2 - 4$ or $(x+2)^2=4/3$ or $x=-2 \pm \sqrt{4/3}$.
Given this information, we can draw the parabola:
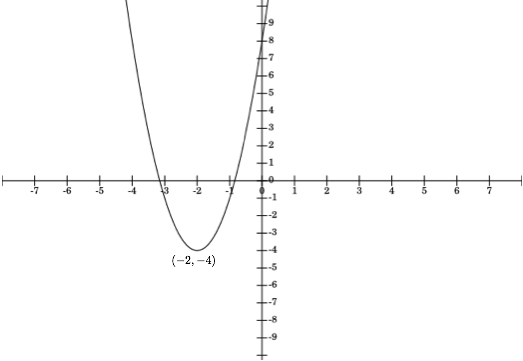
The parabola $y = 3(x + 2)^2 - 4$
