Functions and Their Inverses
Worked Examples
One-to-One Functions
Part 1. What is a one-to-one function?
A function $f$ with domain $A$ is called a one-to-one function if every $f(x)$-value in the range $B$ comes from only one $x$-value in $A$.(i.e. Every element in $A$ is mapped/connected to a unique element in $B$.)
Formally stated: $f$ is $1-1$ if and only if for some $x_1, x_2 \in A,$ $$f(x_1)=f(x_2) \quad implies \quad that \quad x_1=x_2.$$
Example.
Graphically, we can determine if a function is $1-1$ by using the Horizontal Line Test, which states: A graph represents a $1-1$ function if and only if every horizontal line intersects that graph at most once.
Consider the graphs of the functions given in the previous example:
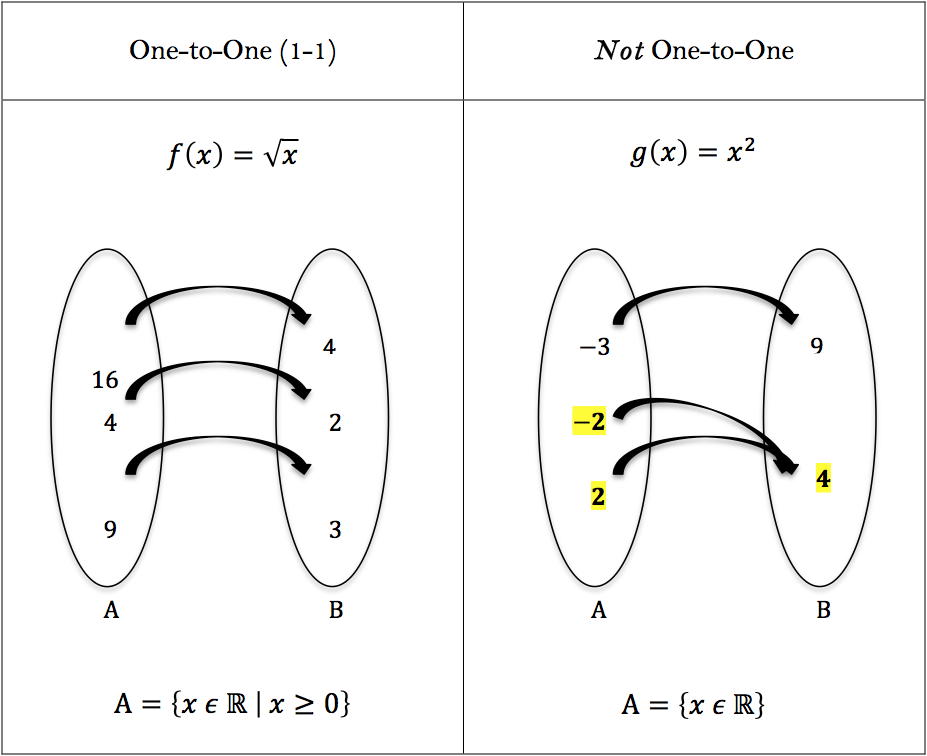
1. $f(x)=\sqrt{x}$

From the graph it’s clear that $f(x)$ is $1-1$. This is because every horizontal line (such as the line $y=1$) intersects the graph at most once. More specifically, if a point of intersection exists between $f(x)$ and the line $y=c$, it is of the form $(c,\sqrt{c}).$
2. $g(x) = x^2$

From the graph we can see that $g(x)$ is not $1-1$, because the horizontal line $y=1$ intersects the graph at $(1, 1)$  and $(−1, 1).$ In general, every horizontal line $y=c$ that intersects the graph, intersects it at $(\sqrt{c},-c)$ and $(-\sqrt{c},-c)$ , except at the vertex $(0,0).$
Part 2. Verifying that a function is 1-1
When we say "verify", we generally mean "prove." To prove that a function is $1-1$, we can't just look at the graph, because a graph is a small snapshot of a function, and we generally need to verify $1-1$-ness on the whole domain of a function. So though the Horizontal Line Test is a nice heuristic argument, it's not in itself a proof. For proofs, we have two main options to show a function is $1-1$:Option 1.
Show that if $f(x_1)=f(x_2),$ then $x_1=x_2.$This statement says in words: "If the function has the same value at two points, then the points must be the same." In other words, "If the function has the same value at two points, the points can't be different." And the final rewording is, "The function can't give the same value to two different points."
Thus, this short mathematical statement is precisely the Horizontal Line Test! The graph is $1-1$ if there are no two $x$-values which get assigned the same $y$-value!
Now, let's use this statement to prove a function is $1-1$:
Example. Show that $f(x)=\frac{1}{x}$ is $1-1.$
Assume that there exists some $x_1$ and $x_2,$ such that $f(x_1)=f(x_2)$. i.e. $\frac{1}{x_1} = \frac{1}{x_2}.$ \begin{align*} \textrm{But, }\; \frac{1}{x_1}=\frac{1}{x_2} &\Rightarrow \frac{1}{x_1}-\frac{1}{x_2} = 0 \\ &\Rightarrow \frac{x_1-x_2}{x_1 x_2} = 0 \\ &\Rightarrow \textrm{ the numerator must equal zero! i.e. } x_2 - x_1 = 0 \\ &\Rightarrow x_2 = x_1 \end{align*}Option 2.
To show a function is $1-1,$ we can show that a function is always increasing or always decreasing. Consequently, it will always pass the Horizontal line test!Recall the following definitions:
A function $f$ is increasing on its domain if whenever $x_1< x_2,$ then $f(x_1) < f(x_2).$
i.e. as $x$ gets larger, $f(x)$ also gets larger.
A function $f$ is decreasing on its domain if whenever $x_1< x_2,$ then $f(x_1) > f(x_2).$
i.e. as $x$ gets larger, $f(x)$ gets smaller.
Example. Show that $f(x)=x^3$ is $1-1.$
We know that for $a,b \in \mathbb{R},$ if $a< b \Rightarrow f(a)=a^3 < b^3 = f(b).$ Therefore, $f(x)=x^3$ is an increasing function on its domain, $\mathbb{R}.$ This can also be verified by the graph (below):
Therefore, every horizontal line $y=c$ will only intersect the graph at the point $(c,c^3).$
