Functions and Their Inverses
Worked Examples
Inverse Functions
Part 1. What is an Inverse Function?
Let $f$ be a $1-1$ function with domain $A$ and range $B.$ Then, its inverse function , denoted by $f^{-1},$ has domain $B$ and range $A$ and is defined by: $$f^{-1}(y) = x \Leftrightarrow f(x)=y \textrm{ for any } y\in B$$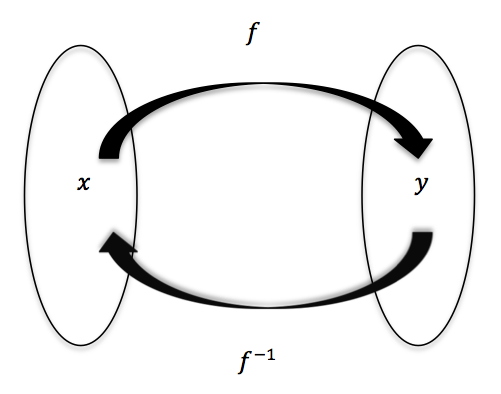
Notice that if $f$ was not $1-1,$ then $f^{-1}$ would be mapping $y$ back to two $x$'s, which would cause $f^{-1}$ to violate the definition of a function! Therefore, inverses only exist for $1-1$ functions!
 Another way of interpreting inverse functions is as follows:
The inverse function of $f$ is simply a rule that undoes $f$'s rule (in the same way that addition and subtraction or multiplication and division are inverse operations.)
Consequently, the range and domain of $f$ and $f^{-1}$ simply switch!
Graphically, this means that any point $(x,y)$ on the graph of $f(x)$corresponds to the point $(y,x)$ on the graph of $f^{-1}(x).$ For example, if $(2,3)$ is on the graph of $f(x),$ then $(3,2)$ is on the graph of $f^{-1}(x).$
Similarly, if $h(-5)=8,$ what is $h^{-1}(8)$?
Well, if $h(-5)=8,$ then the point $(−5,8)$ is on the graph of $h(x).$ This means that, if the inverse function of $h(x)$ exists, the point $(8, −5)$ is on the graph of $h^{-1}(x).$ In other words, if it exists, $h^{-1}(8) = −5.$
From this we can see that the graph of $f^{-1}(x)$ – the inverse function of any function $f(x)$ – is the reflection of the graph of $f(x)$ about the line $y=x.$ (i.e., the $x$-coordinate and $y$-coordinate for each point on the graph switch places!)
Part 2. Cancellation Property of Inverses:
Let $f$ be a $1-1$ function with domain $A,$ range $B,$ and inverse $f^{-1}.$ Then $f$ and $f^{-1}$ satisfy both of the following:| i. | $(f \circ f^{-1})(x) = f(f^{-1}(x)) = x$ | $for \quad every \quad x \in A$ |
| ii. | $(f^{-1} \circ f)(x) = f^{-1}(f(x)) = x$ | $for \quad every \quad x \in B$ |
Example. Consider $f(x)=x+5.$ Find $f^{-1}(x).$
We know that $f$ is the rule that takes a number $x$ and adds $5$ to it. So, in order to undo this rule, we simply need a rule that takes a number $x$ and subtracts $5$ from it. $$ \textrm{i.e. } f^{-1}(x) = x-5 $$ We can verify that we’ve found the correct inverse function by seeing if the Cancellation Property is satisfied: \begin{align*} (f \circ f^{-1})(x) = f(f^{-1}(x)) &= f(x-5) \\ &= (x-5) + 5 \\ &= x - 5 + 5\\ &= x \end{align*}  Similarly, \begin{align*} (f^{-1} \circ f)(x) = f^{-1}(f(x)) &= f^{-1}(x+5) \\ &= (x+5) - 5 \\ &= x + 5 - 5\\ &= x \end{align*}Now, we will consider finding the inverse of more complicated functions:
Example. Let $f(x)=\frac{x+4}{3x-2}.$ Find $f^{-1}(x).$
Notice that it is not as easy to identify the inverse of a function of this form. So, consider the following step-by-step approach to finding an inverse:| Step 1: | Replace $f(x)$ with $y.$ (This is simply to write less as we proceed) $$y =\frac{x+4}{3x-2}$$ |
| Step 2: | Switch the roles of $x$ and $y.$ $$x =\frac{y+4}{3x-2}$$ |
| Step 3: | Solve for $y,$ which will be the desired inverse function. \begin{align*} x =\frac{y+4}{3x-2} & \Rightarrow x(3y-2)=y+4 \\ &\Rightarrow 3xy-2x = y+4 \\ &\Rightarrow 3xy -y = 4 + 2x \\ &\Rightarrow y(3x-1) = 4+2x \\ &\Rightarrow y = \frac{4+2x}{3x-1} \end{align*} |
Again, we can verify that the Cancellation Properties are satisfied: \begin{align*} (f \circ f^{-1})(x) = f(f^{-1}(x)) &= f\left( \frac{4+2x}{3x-1}\right) \\ &=\frac{\left( \frac{4+2x}{3x-1} \right) + 4}{3\left( \frac{4+2x}{3x-1} \right) -2} \\ &= \frac{\left( \frac{4+2x+4(3x-1)}{3x-1} \right) }{\left( \frac{ 3(4+2x) - 2(3x-1) }{3x-1} \right)} \\ &= \frac{\left( \frac{4+2x+12x-4)}{3x-1} \right) }{\left( \frac{ 12+6x - 6x+2) }{3x-1} \right)} \\ &= \frac{\cancel{14}x}{\cancel{3x-1}} \cdot \frac{\cancel{3x-1}}{\cancel{14}} \\ &= x \end{align*}  As an exercise: Try on your own to confirm that $(f^{-1}\circ f)(x) = x$ as well.
Part 3. Restricting Domains of non $1-1$ Functions
Recall that in the first example we saw that $f(x) = x^2$ is not a $1-1$ function for $x \in \mathbb{R}.$ Therefore, it cannot have an inverse over its domain! However, if we restrict the domain to $x \geq 0$ or $x \leq 0,$ the function will be $1-1.$ From the graphs below, we can see that the respective "branches" of the parabola will pass the Horizontal Line Test.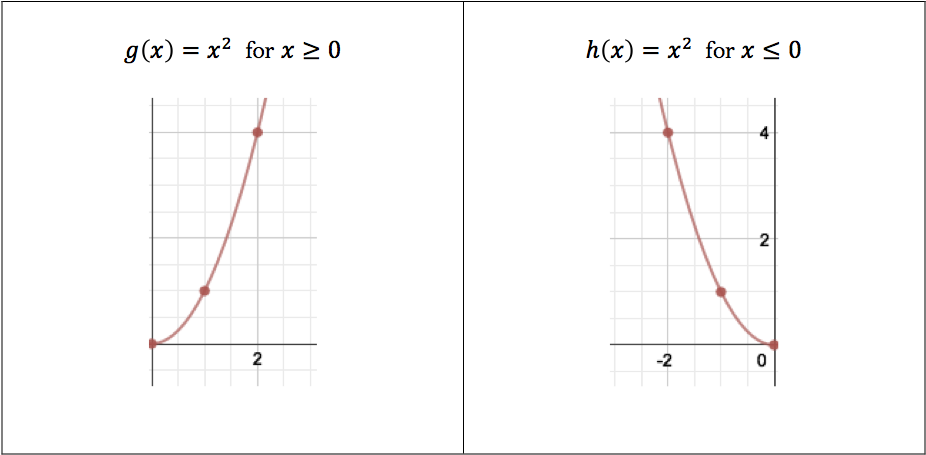
So for these restricted functions: $$g(x) = x^2 \textrm{ for } x \geq 0 \qquad \textrm{ and } \qquad h(x) = x^2 \textrm{ for } x \leq 0,$$ we can find an inverse. Consider $g(x):$
| Step 1: | Replace $g(x)$ with $y:$ $$y = x^2 \qquad \textrm{ for } x \geq 0$$ |
| Step 2: | Switch the roles of $x$ and $y:$ $$x = y^2 \qquad \textrm{ for } y \geq 0$$ |
| Step 3: | Solve for $y,$ such that $y \geq 0:$ \begin{align*} x = y^2 & \Rightarrow y = \pm \sqrt{x} \\ &\Rightarrow y = +\sqrt{x}, \textrm{ since we require } y \geq 0 \\ &\Rightarrow g^{-1}(x) = \sqrt{x} \end{align*} |
