Inequalities
Worked Examples
Half-planes
Recall that a non-vertical line is described by the equation $y=mx+b$. Notice that a straight line divides the plane into two parts. The best way to describe the two parts is by inequalities.The set of point $(x,y)$ in the plane that satisfy the inequality $y < mx + b$ form the half plane "below" the line $y=mx+b$. While the set of points $(x,y)$ in the plane that satisfy the inequality $y > mx+b$ form the half-plane "above" the line $y=mx+b$.
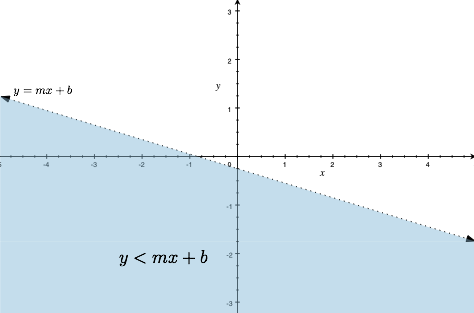
Note that we use a dashed line to indicate that the points on the line are not included in half-planes. If we change the strict inequality $<$ to $\leq$, then we include the points on the line as well. We use a solid line to indicate that these points are included. Similarly, if we change $<$ to $\geq$ we then include the points on the line.
Example. Solve the inequality $y < x$, and sketch the solution.
The set of points that satisfy this equation are those whose x-coordinate is larger than y-coordinate. Consider the line $y=x$. The inequality $<$ tells us that we want the points below the line $y=x$, and that agrees with having a larger x-coordinate than y-coordinate.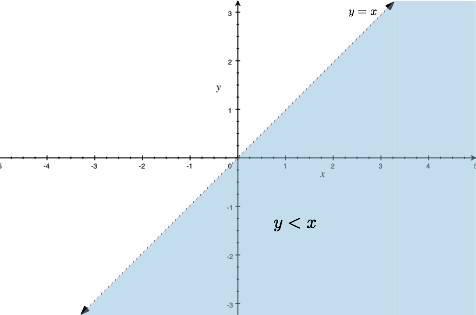
Let's try a more complicated example.
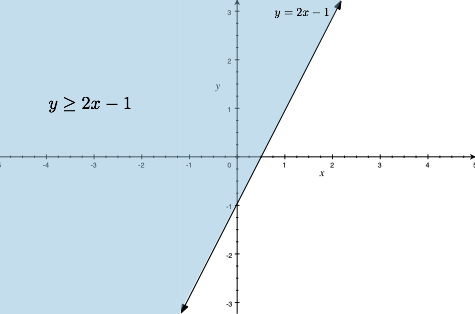
Example. Solve the inequality $x-2y \leq -3x+2$, and sketch the solution.
First, let's rewrite the equation so that we can use what we know:| $ x-2y \leq -3x+2 $ | ||
| $ -2y \leq -4x+2 $ | (Details) subtract $x$ from both sides | |
| $y \geq 2x-1 $ | (Details)divide both sides by $-2$, which switches the inequality |