Inequalities
Worked Examples
Absolute Value
For any real number $a$, $|a|$ is the distance from $a$ to $0$ on the number line.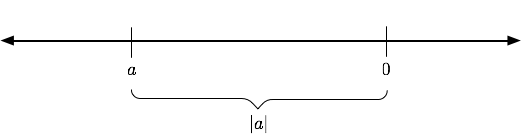
This means that the distance between $a$ and $b$ on the number line is given by $|b-a|$.
Alternatively, we can define $|a|$ as follows: If $a \geq 0$, then $|a| = a$, and if $a <0$, then $|a| = -a$.
We can also define $|a|$ by $|a| = \sqrt{a^{2}}$ where we take the positive square root.
Notice that for any $a \in \mathbb{R}$, $|a| \geq 0$, and $|a| = 0$ if and only if $a=0$.
All of the definitions are equivalent, and useful for various problems. For solving inequalities, the first definition is particularly useful.
Consider an inequality of the form $|x| < r$. From the first definition, we see that the solution set is the set of points whose distance from $0$ is less than $r$. In other words, the solution set is the interval $(-r, r)$.
To see this algebraically, note that $|x| < r$ is equivalent to the double inequality $-r < x < r$, which is exactly the interval $(-r, r)$.

The solution set of an inequality of the form $|x|>r$, is the set of points whose distance from $0$ is larger than $r$. In other words, the solution set is $(-\infty , -r) \cup (r, \infty)$.

Now consider an inequality of the form $|x-a| < r$. The solution set is the set of points whose distance from $a$ is less than $r$.
Algebraically, we get $-r < x-a < r \; $ or $\; a-r < x < a+r$, which is exactly the interval $(a-r, a+r)$.

Mini-Lecture.
Below is a mini lecture about absolute values.
Example. Solve the inequality $4 < | 2x+10| \leq 6$, sketch the solution set on the number line, and express it in interval form.
To deal with an inequality of this form, we should split it into two separate inequalities $4 < | 2x+10|$ and $| 2x+10| \leq 6$, then take the common solutions.First we deal with the inequality $4 < | 2x+10|$:
| $ 4 < | 2x+10| $ | ||
| $ 2 < |x+5| $ | (Details) divide both sides by 2 | |
| $ 2 < |x - (-5)| $ | (Details)re-write it so that we can identify the solution set |

Now we deal with the inequality $| 2x+10| \leq 6$:
| $ | 2x+10| \leq 6 $ | ||
| $ |x+5| \leq 3 $ | (Details) divide both sides by 2 | |
| $ |x - (-5)| \leq 3 $ | (Details)re-write it so that we can identify the solution set |

Now let's put this together. If we sketch the solutions to the inequalities we get:

From this we see that the common solutions are exactly $[-8, -7) \cup (-3, -2]$.
