Round 18

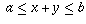Problem 1/18. Determine the minimum length of the interval [a,b] such that (IMAGE)

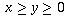for all real numbers (IMAGE)

for which 19x + 95y = 1995.

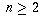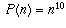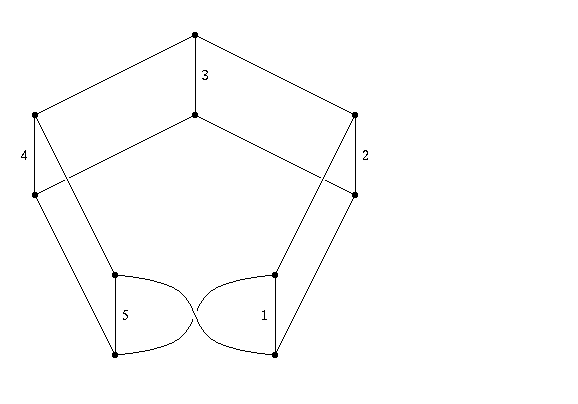
Problem 2/18. For a positive integer (IMAGE) , let P(n) denote the product of the positive integer divisors (including 1 and n) of n. Find the smallest n for which (IMAGE) .

Problem 3/18. The graph shown below has 10 vertices, 15 edges, and each vertex is of order 3 (i.e., at each vertex 3 edges meet). Some of the edges are labelled 1, 2, 3, 4, 5 as shown. Prove that it is possible to label the remaining edges 6, 7, 8, . . . , 15 so that at each vertex the sum of the labels on the edges meeting at that vertex is the same.

(IMAGE)

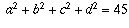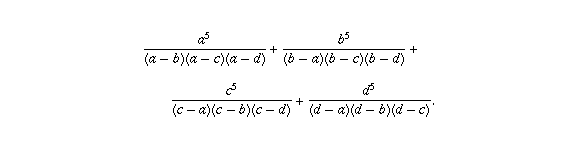
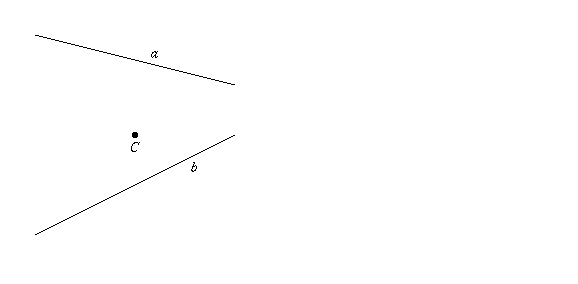
Problem 4/18. Let a, b, c, d be distinct real numbers such that a+b+c+d = 3 and (IMAGE) . Find the value of the expression

(IMAGE)

Problem 5/18. Let a and b be two lines in the plane, and let C be a point, as shown below. Using only a compass and an unmarked straightedge, construct an isosceles right triangle ABC, so that A is on line a, B is on line b, and AB is the hypotenuse of triangle ABC.

(IMAGE)

Solve as many of the problems as you can (you need not solve them all), and mail your solutions to:

Professor E. J. Barbeau
Department of Mathematics
University of Toronto
Toronto, ON M5S 3G3

Make sure that the front page of your solutions contains your full name and mailing address.

These problems are made available through the quarterly journal Mathematics and Informatics. Student subscriptions at US$12 (student rate) or US$18 (teacher rate) may be ordered from Prof. George Berzsenyi, Department of Mathematics, Box 121, Rose-Hulman Institute of Technology, Terre Haute, IN 47803-3999, U.S.A. Remittances should be payable to Mathematics and Informatics.

This page last updated: February 3, 1997
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Current Network Coordinator and Contact Person: Joel Chan - mathnet@math.toronto.edu

Navigation Panel:

$(SWITCH TO TEXT-ONLY VERSION)$

Go backward to Round 17
Go up to Talent Search Index
Go forward to Round 19
$(SWITCH TO TEXT-ONLY VERSION)$ Switch to text-only version (no graphics)
Access printed version in PostScript format (requires PostScript printer)
Go to University of Toronto Mathematics Network Home Page