International Mathematical Talent Search
International Mathematical Talent Search
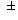 signs below by either - or + so that
signs below by either - or + so that
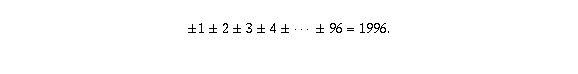
At most how many of the +/- signs can be replaced by a + sign?
Problem 2/19. We say that (a,b,c) is a primitive Heronian triple if a, b, and c are positive integers with no common factors (other than 1), and if the area of the triangle whose sides measure a, b, and c is also an integer. Prove that if a=96, then b and c must both be odd.
Problem 3/19. The numbers in the 7 by 8 rectangle shown below were obtained by putting together the 28 distinct dominoes of a standard set, recording the number of dots (ranging from 0 to 6) on each side of the dominoes, and then erasing the boundaries among them. Determine the original boundaries among the dominoes. (Note: each domino consists of two adjoint squares, referred to as its sides).
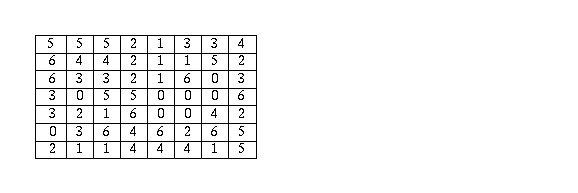
Problem 4/19. Suppose that f satisfies the functional equation
Find f(3).
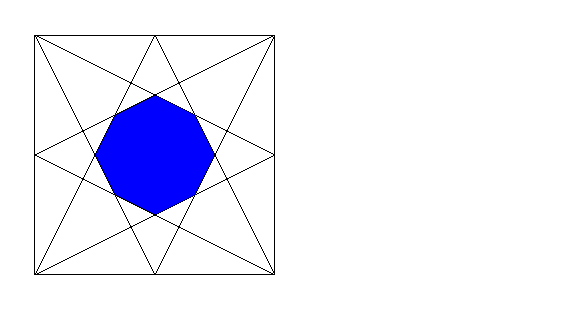
Problem 5/19. In the figure below, determine the area of the shaded octagon as a fraction of the area of the square, where the boundaries of the octagon are lines drawn from the vertices of the square to the midpoints of the opposite sides.
Solve as many of the problems as you can (you need not solve them all), and mail your solutions to:
Professor E. J. BarbeauMake sure that the front page of your solutions contains your full name and mailing address.
Department of Mathematics
University of Toronto
Toronto, ON M5S 3G3
![]() Go backward to Round 18
Go backward to Round 18![]() Go up to Talent Search Index
Go up to Talent Search Index![]() Go forward to Round 20
Go forward to Round 20![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page