October 1997 Presentation Topic (continued)

Solution to Question 3 (the hard problem)

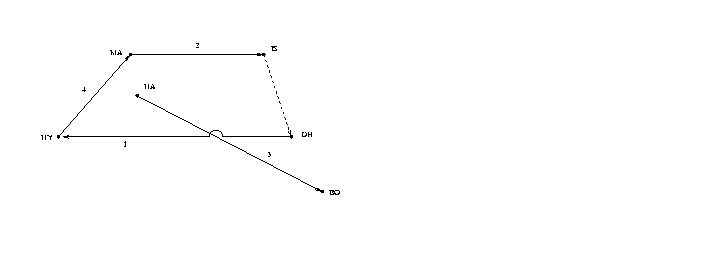
Observe that routes have been numbered according to the statement of the problem.

Also observe that in order to make shipping a continuous steady state process, to have one ship per day arriving (or leaving) a given port, there will have to be a queue of ships spaced one day apart along the adjoining route. Furthermore, once a ship has finished a cargo route, it may have to travel empty to another port in order to begin another route.

For example, in order to have 1 ship per day shifting from route 2 to route 1, there will need to be a queue of 10 ships spaced out along the itinerary MA -> IS ->DH. This is because it takes a ship 10 days from the time it begins route 2 until the time it is ready to begin route 1: 1 day loading cargo at Marseilles, 3 days travelling along route 2 to Istanbul, 1 day unloading at Istanbul, and 5 days travelling empty from Istanbul to Dhahran in preparation for beginning route 1.

In general, in order to have 1 ship per day shifting from route i to route j, there must always be a queue of 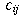ships involved in servicing route i then travelling to begin route j, where 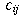is 2 plus the time taken to travel route i plus the time taken to travel from the endpoint of route i to the starting point of route j.

The values of 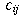are tabulated below:

If we let 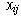be the number of ships shifting from route i to route j daily, then the total number of ships servicing route i at any one time (where "servicing route i" includes getting ready for the next route after finishing route i) is

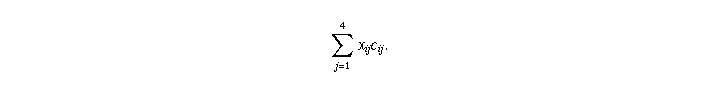
Our goal is to choose the 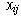so as to minimize the total number of ships, which is

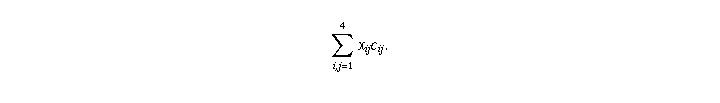
The only constraints are that the daily number of ships completing a route must equal the daily number of ships beginning it, and this must equal the number specified in the problem (3 for route 1, 2 for route 2, and 1 for routes 3 and 4).

Under our definition for 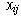, 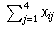yields the daily number of ships completing route i. This gives constraints , , , .

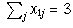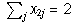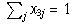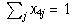Similarly 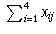yields the daily number of ships beginning route i. This gives constraints , , , .

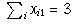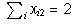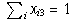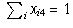Eureka! a transportation problem of modest size. Its solution is

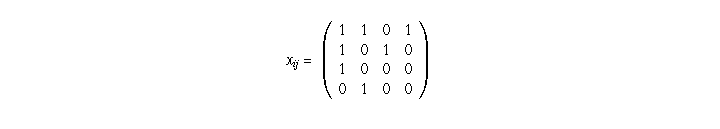
Which we interpret as follows:

Of the three ships servicing route 1 daily, one goes back to begin route 1 again, one goes on to route 1, and one goes on to route 4. Referring back to the table for 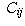, this means that at any given time

• 36 ships are occupied travelling route 1 (DH -> NY) then returning empty in preperation for another route 1 trip.

• 32 ships are occupied travelling route 1 then going empty to MA in preparation for a route 2 (MA -> IS) cargo journey;

• 19 ships are occupied travelling route 1 then reloading in preparation for a loaded journey to MA (route 4).

Similarly, we find that, at any given time,

• 10 ships are occupied travelling route 2 (MA -> IS) then going empty to DH in preparation for a route 1 (DH -> NY) cargo journey;

• 7 ships are occupied travelling route 2 then going empty to NA in preparation for a route 3 (NA -> BO) cargo journey;

• 12 ships are occupied travelling route 3 (NA -> BO) then going empty to DH in preparation for a route 1 (DH -> NY) cargo journey;

• 15 ships are occupied travelling route 4 (NY -> MA) then reloading in in preparation for a route 2 (MA -> IS) cargo journey.

Thus, 131 ships are needed in all.

Go backward to Problems
Go up to Introduction and Contents
Switch to text-only version (no graphics)
Access printed version in PostScript format (requires PostScript printer)
Go to SIMMER Home Page
Go to The Fields Institute Home Page
Go to University of Toronto Mathematics Network Home Page