
May 1997 Presentation Topic (continued)



May 1997 Presentation Topic (continued)
Algebra over the integers is already an interesting subject. We
call an integer p a prime number if its only divisors are
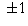 and
and 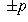 . (Exception: the numbers
. (Exception: the numbers 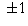 themselves
are not called prime; they are called units instead).
themselves
are not called prime; they are called units instead).
Question 1: Can you show that there are infinitely many prime numbers?
There are many interesting questions about prime numbers. For instance, are there any primes with 100 digits? How many primes like this are there? These questions have become more important in recent years since constructing (and breaking!) many computer security systems depends on being able to factor huge numbers.
Question 2: Using a line segment (designated to be of
length one), a straight edge and a compass, construct the
diagonal of a square of side length one. That is, using these
tools (all available to the Greeks!), construct a line segment
that is the diagonal of a square of side length one. Can you show
that this side length is not a rational multiple of the unit
length? Phrased another way, can you show that  is not
a rational number?
is not
a rational number?
When this fact was discovered, it caused quite a sensation. Not only was a mathematical idea proven incorrect, but a whole philosophy was discredited.
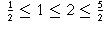 . I hope to show you later that ordering numbers is
actually a rather difficult and deep problem.
. I hope to show you later that ordering numbers is
actually a rather difficult and deep problem.
The positive integers have a nice property: there is a smallest positive integer (namely, 1). In fact, even if you throw away the number 1, or even if you throw away a whole collection of numbers (as long as you don't throw them all away!), there will still be among the remaining numbers one which is the smallest. This is called the well-ordering principle.
However, the rational numbers with their natural ordering do not satisfy the well-ordering principle.
Question 3: Show that there is no smallest positive rational number. This suggests that the Greek notion of an atom (a smallest indivisible amount) might not exist.
It is a surprising result from set theory that every set admits a well-ordering. Therefore, we can order the positive rational numbers in such a way that (a) for any two distinct numbers, one is larger than the other; and (b) in any collection of numbers (other than the empty set, of course), there's always a smallest number. However, this ordering is not at all the same as the usual ordering!
Question 4: Try to find an ordering on the positive rational numbers which has these properties.
Question 5: Show that 0.999. . . = 1. We say there are two ways to represent the number 1 in decimal notation. Are there any other ways to represent the number 1 in decimal notation?
This suggests that real numbers are much more complicated than
ordinary old rational numbers. It is quite hard to get a hold of
a real number: we need to know all of its digits. This really
disturbed me when I was first learning mathematics. If this is
the case, in what sense do we know that the number
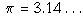 exists?
exists?
Question 6: Two monkeys (Abe and Bonzo) come upon a clearing containing two barrels (A and B) and an infinite number of coconuts, conveniently labeled with the positive integers. Abe suggests two ways of filling the barrels. The monkeys can do this very fast, so that we can ask what will happen when ALL the coconuts are in the barrels. Which method should Bonzo agree to?
Intuitively it seems obvious that there are more real numbers than rational numbers and more rational numbers than integers. What do you think about the relative sizes of such infinite collections of numbers? In what sense do we mean that there are more reals than integers? These are interesting questions to ponder.
We'll discuss this, and other similar problems, in terms of formulas known to ancient Chinese mathematicians. We'll also explain how modern mathematics studies these problems using modular arithmetic.
In the integers modulo 7, there are only seven numbers: 0, 1, 2, 3, 4, 5, and 6. You can divide 3 by 2 in this number system: the quotient is 5, since 2 times 5 equals 3 in arithmetic modulo 7.
Question 8: Try to show that you can always divide any number by any non-zero number, in the integers modulo 7. Can this still be done in the integers modulo 12?
Question 9: In the integers modulo 7, compute
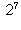 ,
, 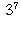 and
and 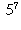 (there is a clever way to
do this last one). What do you notice? Can you prove your
conjecture?
(there is a clever way to
do this last one). What do you notice? Can you prove your
conjecture?


![]() Go up to Introduction and Contents
Go up to Introduction and Contents![]() Go forward to Solutions
Go forward to Solutions![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer) Go to SIMMER Home Page
Go to SIMMER Home Page Go to The Fields Institute Home Page
Go to The Fields Institute Home Page![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page