
Society Investigating Mathematical Mind-Expanding Recreations



Society Investigating Mathematical Mind-Expanding Recreations
Examples
Stranger surfaces can be created which cannot be embedded in three-dimensional space; examples are the Klein bottle and the projective plane, which we'll see later. Also, two surfaces may be joined together to form their connected sum. For example, the connected sum of two tori is the two-holed torus.
How can we predict what will happen if we cut a surface apart, join two surfaces together, or perform any other such "surgery"? How can we tell when it is possible to transform one surface into another? One way of approaching such questions is through the use of plane diagrams to represent the surfaces.
As an example of the utility of plane diagrams, we use them to represent the slicing of a surface along a curve on the surface.
Problem 1: Using the plane diagram for the Möbius band, predict the outcome of cutting the surface down the middle (laterally). Verify experimentally. Then repeat the experiment, this time cutting the surface starting one-third of the way across.
Problem 2: Find a way to cut the Klein bottle to get (i) a Möbius band, and (ii) two Möbius bands.
We next show how to join two surfaces together, (i.e. perform connected sums) by way of their plane diagrams.
Problem 3: Find a plane diagram for the two-holed torus, then the three-holed torus. Try to find a pattern, and find a plane diagram for the general n-holed torus.
Problem 4: Show that the Klein bottle is the connected sum of two projective planes.
In fact, the last problem is just a consequence of the classification theorem, which states that any surface is either a sphere, or the connected sum of tori, or the connected sum of projective planes.
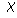 .
It is important in the study of surfaces not only because it is an invariant
(that is, if two surfaces are topologically equivalent, then their Euler
characteristics are equal), but also because it is easily computed, in contrast
to some other invariants.
.
It is important in the study of surfaces not only because it is an invariant
(that is, if two surfaces are topologically equivalent, then their Euler
characteristics are equal), but also because it is easily computed, in contrast
to some other invariants.
We can calculate the Euler characteristic of a surface by looking at its plane diagram. For example, the characteristic of a sphere is 2, while that of a torus is 0.
Problem 5: Find the Euler characteristic for the projective plane, the Klein bottle, and the two-holed torus, the n-holed torus, and the connected sum of n projective planes.
Problem 6: Show that the two-holed torus and the connected sum of the one-holed torus and the projective plane are not topologically equivalent.
Problem 7: Compare the Euler characteristics of the torus to that of the Klein bottle. Are the two surfaces topologically equivalent? Why or why not?


![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer) Go to SIMMER Home Page
Go to SIMMER Home Page Go to The Fields Institute Home Page
Go to The Fields Institute Home Page![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page