Question Corner and Discussion Area
Question Corner and Discussion Area
The tetrahedronal numbers: 1, 4, 10, 20, 35, . . . are derived by adding the triangular numbers: 1 + 3 + 6 + 10 + 15 + · · · + (n)(n+1)/2. At one time I derived a formula for the sum through the mth term of the tetrahedronal numbers, and also the sum of the numbers for a 4-tetrahedron: 1, 5, 15, 35, 70, . . . , which are of course the sum of the tetrahedronal numbers. (Tetrahedronal numbers are best described by placing larger and larger triangular layers of 3-spheres under the previous triangular layer of spheres, forming a tetrahedronal pyramid.) Can you provide these formulas? Thanks.These numbers are all expressible as binomial coefficients. If we let
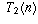 denote the nth triangular number,
denote the nth triangular number,
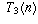 the nth tetrahedral number, and so on, then
the nth tetrahedral number, and so on, then
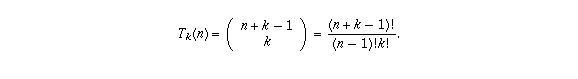
You can prove this by induction noting that each 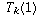 equals
1, that the formula is correct when k=2, and
the difference
equals
1, that the formula is correct when k=2, and
the difference 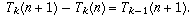
You could also prove this by a more "brute-force" approach, using the formulas for the sums of powers:
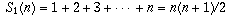
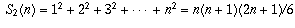
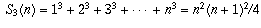
and so on. To arrive at these
formulas you can again proceed by brute force (make the intelligent guess
that 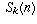 should be a polynomial of degree n+1 and plug in enough
values to solve for the coefficients), or else employ a trick like the
following:
should be a polynomial of degree n+1 and plug in enough
values to solve for the coefficients), or else employ a trick like the
following:
Write 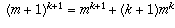 plus terms involving
lower powers of m. When you add up the LHS as m ranges from 0 to n,
you get
plus terms involving
lower powers of m. When you add up the LHS as m ranges from 0 to n,
you get 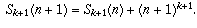 When you add up
the RHS, you get
When you add up
the RHS, you get 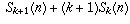 plus terms involving
plus terms involving
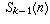 down through
down through 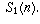 This gives you
This gives you
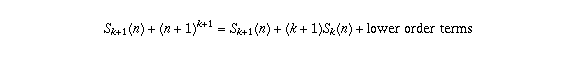
The terms 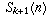 cancel, and you are left with a formula
that expresses
cancel, and you are left with a formula
that expresses 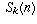 in terms of
in terms of 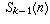 down through
down through
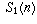 .
.
For example, here is how to use the above technique to arrive at the
formula for  :
:
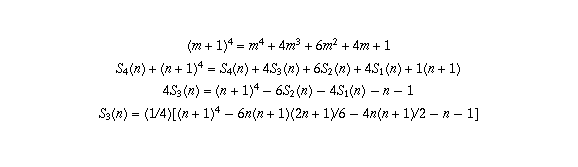
and simplifying gives the above formula. (Note that the reason n+1 appears at the end of the second line is that we are adding up the first line as m ranges from 0 to n; that means the final constant term "1" is added up n+1 times.)
Now that you have formulas for S_k(n), it is easy to find formulas for the tetrahedral numbers. For example,
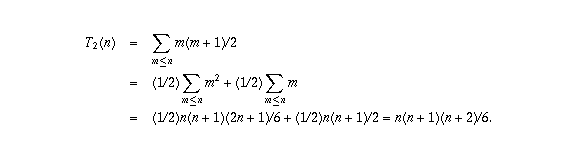
![]() Go backward to Calculating Digits of Pi in Other Bases
Go backward to Calculating Digits of Pi in Other Bases![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Existence of Shapes with Irrational Dimensions
Go forward to Existence of Shapes with Irrational Dimensions![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page