(These buttons explained below)
Question Corner and Discussion Area
If a person has $150,000 and it compounds at, let's say, eight per-cent per year, and that person (while all this is taking place) draws $1,200 monthly from the fund, how long will the fund last until it is exhausted??? Is there a formula I can use to determine the time/amounts based on compounded interest etc.??? For example, if it was $175,000 at 9 per-cent. . . how many years when drawing out $1,300 per month?? I suspect you have a simple formula or way of doing it????? Appreciate it if you could e mail me your suggestion (short of taking a math class.) Thanks.Your question is actually the same as the principles used in mortgage calculation. Here is how to derive the formulas:
Suppose the monthly interest rate is I, and that an amount W is withdrawn each month. What this means is that, during each month, the balance gets multiplied by 1+I (it becomes the original amount plus the interest, which is I times the original amount) and then has W subtracted from it.
Therefore, if B(0) is the starting balance, the balance after one month will be
B(1) = (1+I)B(0) - W.For convenience, let J denote 1+I, so that B(1) = J B(0) - W. After two months the balance will be
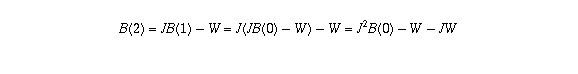
and in general, after n months the balance will be
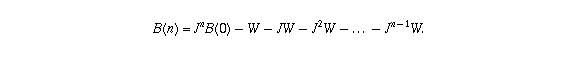
There's a convenient formula for the sum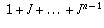 
: it
is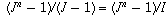 
. Therefore, abbreviating the starting
balance B(0) to just "B",
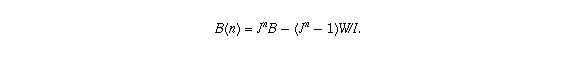
Your question is asking how large n has to be before the balance drops to zero; in other words, you want to solve for n in the equation
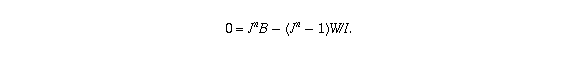
Some basic algebra lets you rewrite this equation as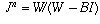 
;
taking logarithms of both sides gives
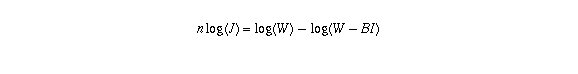
so
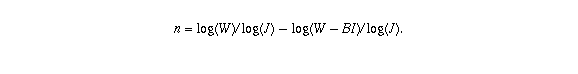
The only other thing you need to know before being able to solve your problems
is what the monthly interest rate is. The monthly interest rate I and
annual rate A are related by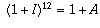 
(because your balance
is multiplied by 1+I each month and hence is multiplied by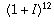 
each year, but we also know that each year it is multiplied by 1+A, so
these two factors must be equal).
Therefore,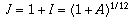 
.
In your first example, A = 0.08 (8 percent), so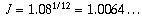 
and I is roughly 0.0064. You have W = 1200 and
B = 150000. Plugging these into the above formula gives
n = 254.30. . .so the account would be exhausted during the 255th month (during the 22nd year).
In your second example, A = 0.09, W = 1300, B=175000, giving n = 489.28. . . so the account would be exhausted during the 41st year.
These formulas are usually used in mortgage calculations: the amount you owe is increased by the interest accruing on it, but is reduced by each of your monthly payments W (just as, in your example, your bank account increases by the interest earned but is recuced by your monthly withdrawals). In mortgages, however, n is known and W is what needs to be calculated. For example, in a 25-year mortgage at 8% on $100,000, the bank needs to calculate a monthly payment amount W which will reduce the balance to zero after n=300 months. So the equation
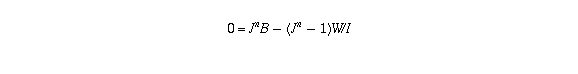
needs to be solved for W. The solution is
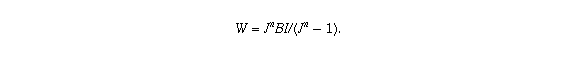
In this example, n=300, B = 100,000, J = 1.0064. . . and I=0.0064. . . , yielding W = 753.415. . . . Your monthly payments on such a mortgage would be $753.42.
Go backward to How To Compute Standings In Baseball Go up to Question Corner Index Go forward to Applications of the Geometric Mean Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page