(These buttons explained below)
Question Corner and Discussion Area
In sports statistics, namely baseball, how do you calculate the number of games that a second place team is behind the first place team? This is easy if both teams have played the same number of games, but if they have not played the same amount, it isn't so clear. This sounds like a fascinating mathematical question for a math fan and sports buff. I have come up with a few scenarios, but never have seen a definitive formula.The standard way to interpret the number of games one team is behind another is as the number of games in which that team would have to beat the other team in order for their standings to become equal.I apologize if this is not the correct forum for this, but I haven't found anything yet that is. Please let me know where I can find this answer elsewhere. Your web pages seem to be a wealth of statistical and mathematical knowledge. I need to solve this dilemma for a league that I am administering.
Thanks.
This number is always an integer when the teams have played the same number of games. However, when the number of games played is unequal, it's convenient to consider fractions of games. For instance, if team I has won 9 and lost 10, while team II has won 10 and lost 10, we say that team I is half a game behind team II (because if team I played and beat team II in one full game, team I then be as much ahead of team II as it used to be behind).
One way to interpret this mathematically is the following. Suppose that Team I has won w games and lost l games and Team II has won W games and lost L games. Their winning averages (wins per games played) are w/(w+l) and W/(W+L) respectively.
We say that Team I is n games behind Team II if adding n more wins
to Team I and n more losses to Team II would cause their winning averages
to become equal; in other words, if
.
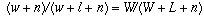Solving for n we get that
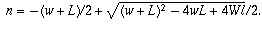Admittedly this formula looks complex, though it gets directly to the point
by setting the winning averages of the two teams
to be equal after n Team I versus Team II games
are won by Team I.
The output of the formula will also need to be rounded to the nearest half game to make the statistics "look nice" and be consistent with the usual practice. For instance, if team I has a 10-and-10 record while team II has a 10-and-9 record, the above formula gives n=0.51249. . . and we would normally consider the number of games behind to be 1/2.
Go backward to How To Build A Parabolic Dish Go up to Question Corner Index Go forward to Regular Withdrawals on Compound Interest Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page