Answers and Explanations
Answers and Explanations
What if the simple interest isn't 100%? In other words, suppose your money wouldn't have doubled under simple interest, but increased by some other factor?
Suppose for instance the simple interest is 200%. Then we can split the time period up into two halves, with the simple interest being 100% for each half (for example, if you earn 200% simple interest per year, you're earning 100% interest for each six-month period).
At the end of the first half and the beginning of the second half, the balance under compound interest will be e times the original balance.
At the end of the second half, the balance under compound interest will be e times the balance at the beginning of the second half. In other words, it will be
e times (e times original amount)which is
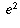 times the original amount. So, if the
simple interest earned is 200% (2 times original amount), the final
balance under compound interest is
times the original amount. So, if the
simple interest earned is 200% (2 times original amount), the final
balance under compound interest is 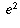 times the original
amount.
times the original
amount.
This turns out to be true in general. If the simple interest earned is
R times the original balance, then the final balance under
compound interest is 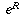 times the original balance.
times the original balance.
This is one of the reasons why exponentials of the form 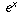 occur
more frequently in practice than do exponentials with other bases such
as
occur
more frequently in practice than do exponentials with other bases such
as 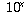 , and why one usually uses exponentials and logarithms
base e rather than base 10 or any other base. (The other, more
important, reason has to do with the special role that base e
exponentials play in calculus).
, and why one usually uses exponentials and logarithms
base e rather than base 10 or any other base. (The other, more
important, reason has to do with the special role that base e
exponentials play in calculus).
[Go on]
![]() Go backward to Simple and Compound Interest
Go backward to Simple and Compound Interest![]() Go up to Does the Number e Have Special Meaning?
Go up to Does the Number e Have Special Meaning?![]() Go forward to The Number e as a Limit
Go forward to The Number e as a Limit![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page