Answers and Explanations
Answers and Explanations
Suppose the simple interest rate is 100% for a certain period. Under simple interest alone, the money will double during that period. Under continually compounding interest, it will be multiplied by e. But what happens if interest is compounded at n equally spaced dates during that period (such as at the and of each month), rather than continually?
In the interval before the first compounding date, you are just earning simple interest on the original balance. Let's call the original balance B. The interest rate for this interval is 1/n, since the total interest rate for all n intervals is 1 (100% is just another way of writing 1). So, on the first compounding date, one gets paid interest in the amount of (1/n)B. The balance after this payment is therefore B + (1/n)B which equals (1 + (1/n)) B. In other words:
(balance at end of first interval) = (1 + (1/n)) times (balance at start of first interval)During the second interval (between the first and second compounding dates), one is again earning interest at a rate of 1/n, but this time on this new balance (1 + (1/n))B. Therefore,
= (1 + (1/n)) B.
(balance at end of second interval) = (1 + (1/n)) times (balance at start of second interval)If you do this same calculation again, you find that the balance at the end of the third interval is
= (1 + (1/n)) times (1 + (1/n)) B
=.
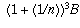 and so
on. The balance at the end of the nth and final interval is
and so
on. The balance at the end of the nth and final interval is
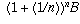 .
.
Therefore: if the interest is compounded n times during the
period, the final balance is 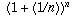 times the
original balance.
times the
original balance.
Compounding at more and more frequent intervals means that one is approximating more and more closely the idea of continual compounding which we talked about earlier, in which the final balance is e times the original balance. What this means is that
The number e is the limit of the quantity 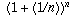 as n goes to infinity.
as n goes to infinity.
This gives a nice mathematical definition of the number e.
[Go On]
![]() Go backward to The General Situation
Go backward to The General Situation![]() Go up to Does the Number e Have Special Meaning?
Go up to Does the Number e Have Special Meaning?![]() Go forward to The Number e in Calculus
Go forward to The Number e in Calculus![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page