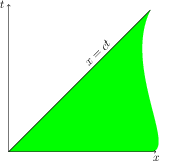
Consider wave equation in domain $\{x>0, t>0\}$ and initial conditions \begin{align} &u_{tt}-c^2 u_{xx}=0 \qquad &&x>0,\ t>0\label{eq-1}\\ &u|_{t=0}=g(x) && x>0,\label{eq-2}\\ &u_t|_{t=0}=h(x) && x>0.\label{eq-3} \end{align} Here we take $f(x,t)=0$ for simplicity. Then according to the previous lecture solution $u(x,t)$ is defined uniquely in the domain $\{t>0, x \ge ct\}$:

where it is given by D'Alembert formula \begin{equation} u(x,t)= \frac{1}{2}\bigl[ g(x+ct)+g(x-ct)\bigr]+\frac{1}{2c}\int_{x-ct}^{x+ct} h(x')\,dx'. \label{eq-4} \end{equation} What about $\{0 < x < ct\} $? We claim that we need one boundary condition as $x=0, t>0$. Really, recall that the general solution of (\ref{eq-1}) is \begin{equation} u(x,t)= \phi (x+ct)+\psi (x-ct) \label{eq-5} \end{equation} where initial conditions (\ref{eq-2})-(\ref{eq-3}) imply that \begin{align*} &\phi(x)+\psi(x)= g(x),\\ &\phi (x)-\psi(x)=\frac{1}{c}\int^x_0 h(x')\,dx' \end{align*} as $x>0$ (where we integrated the second equation) and then \begin{align} &\phi(x)= \frac{1}{2}g(x)+\frac{1}{2c}\int^x _0 h(x')\,dx',\qquad&&x>0,\label{eq-6}\\ &\psi(x)=\frac{1}{2}g(x)-\frac{1}{2c}\int^x _0 h(x')\,dx'\qquad&&x>0. \label{eq-7} \end{align} So, $\phi(x+ct)$ and $\psi(x-ct)$ are defined as $x+ct>0$ (which is automatic as $x>0,t>0$) and $x-ct<0$ (which is fulfilled only as $x>ct$).
To define $\psi(x-ct)$ as $0< x < ct$ we need to define $\psi(x)$ as $x<0$ and we need a boundary condition as $x=0,t>0$.
Example 1. Consider Dirichlet boundary condition
\begin{equation}
u|_{x=0}= p(t), \qquad t>0.
\label{eq-8}
\end{equation}
Plugging (\ref{eq-4}) we see that $\phi(ct)+\psi(-ct)=p(t)$ as $t>0$ or
equivalently $\phi(-x)+\psi(x)=p(-x/c)$ as $x<0$ (and $-x>0$)
where we plugged $t:=-x/c$. Plugging (\ref{eq-6}) we have
\begin{multline}
\psi(x)=p(-x/c)-\phi(x)=\\
p(-x/c)-\frac{1}{2}g(-x) -\frac{1}{2c}\int_0^{-x} h(x')\,dx'.
\qquad
\label{eq-9}
\end{multline}
Then plugging $x:=x+ct$ into
(\ref{eq-6}) and $x:=x-ct$ into (\ref{eq-9}) and adding we get from
(\ref{eq-4}) that
\begin{multline} u(x,t)=
\underbracket{\frac{1}{2}g(x+ct)+
\frac{1}{2c}\int_0^{x+ct}h(x')\,dx'}_{=\phi(x+ct)}+ \\
\underbracket{p(t-x/c)-\frac{1}{2}g(ct-x)
-\frac{1}{2c}\int_0^{ct-x} h(x')\,dx'}_{=\psi(x-ct)}. \qquad
\label{eq-10}
\end{multline}
This formula defines $u(x,t)$ as
$0
Example 2. Alternatively, consider Neumann boundary condition \begin{equation} u_x|_{x=0}= q(t), \qquad t>0. \label{eq-13} \end{equation}
Plugging (\ref{eq-4}) we see that $\phi'(ct)+\psi'(-ct)=q(t)$ as $t>0$ or equivalently $\phi(-x)-\psi(x)=c\int _0^{-x/c}q(t')\,dt'$ as $x<0$ (and $-x>0$) where we integrated first and then plugged $t:=-x/c$.
Plugging (\ref{eq-6}) we have \begin{multline} \psi(x)=-c\int _0^{-x/c}q(t')\,dt'+\phi(x)=\\ -c\int _0^{-x/c}q(t')\,dt'+\frac{1}{2}g(-x) +\frac{1}{2c}\int_0^{-x} h(x')\,dx'. \qquad \label{eq-14} \end{multline} Then plugging $x:=x+ct$ into (\ref{eq-6}) and $x:=x-ct$ into (\ref{eq-14}) and adding we get from (\ref{eq-4}) that \begin{multline} u(x,t)= \underbracket{\frac{1}{2}g(x+ct)+ \frac{1}{2c}\int_0^{x+ct}h(x')\,dx'}_{=\phi(x+ct)}+ \\ \underbracket{-c\int _0^{t-x/c}q(t')\,dt'+\frac{1}{2}g(ct-x) +\frac{1}{2c}\int_0^{ct-x} h(x')\,dx'}_{=\psi(x-ct)}. \qquad \label{eq-15} \end{multline} This formula defines $u(x,t)$ as $0< x<ct$. Recall that for $x>ct$ solution is given by (\ref{eq-4}).
In particular
Example 3. Alternatively, consider boundary condition \begin{equation} (\alpha u_x+\beta u_t)|_{x=0}= q(t), \qquad t>0. \label{eq-18} \end{equation} Again we get equation to $\psi(-ct)$: $(\alpha -c \beta)\psi'(-ct)+ (\alpha +c \beta) \phi' (ct)=q(t) $ and everything works well as long as $\alpha\ne c\beta $.
Example 4. Alternatively, consider Robin boundary condition \begin{equation} (u_x+\sigma u)|_{x=0}= q(t), \qquad t>0. \label{eq-19} \end{equation} and we get $ \psi'(-ct)+\sigma \psi (-ct) + \phi'(ct)+\sigma \phi (ct)=q(t)$ or equivalently \begin{equation} \psi'(x)+\sigma \psi (x)=q(-x/c)- \phi'(-x)+\sigma \phi (-x) \label{eq-20} \end{equation} where the right-hand expression is known.
In this case we define $\psi(x)$ as $x<0$ solving ODE (\ref{eq-20}) as we know $\psi(0)=\frac{1}{2}g(0)$ from (\ref{eq-7}).
Consider wave equation in domain $\{a< x< b, t>0\}$ and initial conditions \begin{align} &u_{tt}-c^2 u_{xx}=0 \qquad &&a<x<b,\ t>0\label{eq-21}\\ &u|_{t=0}=g(x) && a<x<b,\label{eq-22}\\ &u_t|_{t=0}=h(x) && a<x< b.\label{eq-23} \end{align} Here we take $f(x,t)=0$ for simplicity. Then according to the previous lecture solution $u(x,t)$ is defined uniquely in the characteristic triangle $ABC$.
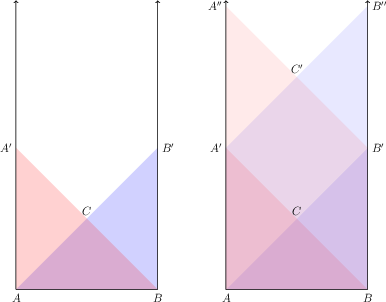
However $\phi (x)$, $\psi(x)$ are defined as $a
Now the boundary condition on the left end (f. e. $u|_{x=a}=p_l(t)$, or $u_x|_{x=a}=q_l(t)$, or more general condition) allows us to find $\psi (a-ct)$ as $0<t<(b-a)/c$ and then $\psi(x-ct)$ is defined in $ABB'';A'$. Similarly the boundary condition on the right end (f. e. $u|_{x=b}=p_r(t)$, or $u_x|_{x=a}=q_r(t)$, or more general condition) allows us to find $\phi (b+ct)$ as $0<t<(b-a)/c$ and then $\phi(x+ct)$ is defined in $ABB'A''$. So, $u$ is defined in the intersection of those two domains which is $AA'C'B'B$.
Continuing this process in steps we define $\phi (x+ct)$, $\psi (x-ct)$ and $u(x,t)$ in expanding “up” set of domains.