$\newcommand{\const}{\mathrm{const}}$
It will be a short lecture as two previous ones were a bit too long.
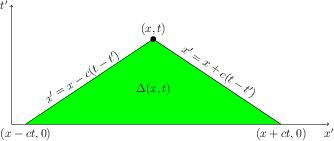
Recall formula (4.4): \begin{multline} u(x,t)= \frac{1}{2}\bigl[ g(x+ct)+g(x-ct)\bigr]+\frac{1}{2c}\int_{x-ct}^{x+ct} h(x')\,dx'+\\[3pt] \frac{1}{2c} \iint_{\Delta (x,t)} f(x',t' )\,dx’d t' \label{equ-6.1} \end{multline} where $\Delta (x,t)$ is a characteristic triangle:

Therefore
Proposition. Solution $u(x,t)$ depends only on the right hand expression $f$ in $\Delta(x,t)$ and on the initial data $g,h$ on the base of $\Delta(x,t)$.
Definition. $\Delta(x,t)$ is a triangle of dependence for point $(x,t)$.
Conversely, if we change functions $g,h$ only near some point $(\bar{x},0)$ then solution can change only at points $(x,t)$ such that $(\bar{x},0)\in \Delta(x,t)$; let $\Delta^+(\bar{x},0)$ be the set of such points $(x,t)$:
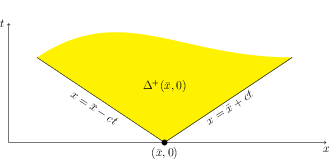
Definition. $\Delta^+(\bar{x},0)$ is a triangle of influence for point $(\bar{x},0)$.
Remark. 1. We can introduce triangle of influence for each point (not necessary at $t=0$). 2. These notions work in much more general settings and we get domain of dependence and domain of influence which would not be triangles. 3. F.e. for $3D$ wave equation $u_{tt}- c^2 (u_{xx}+u_{yy}+u_{zz})=f$ those would be the backward light cone and forward light cone respectively and if $c$ is variable instead of cones we get conoids (imagine tin coin and then deform it but the vertex should remain).
We see also that
Proposition. Solution propagates with the speed not exceeding $c$.
In examples we rewrite the last term in (\ref{equ-6.1}) as a double integral: \begin{multline} u(x,t)= \frac{1}{2}\bigl[ g(x+ct)+g(x-ct)\bigr]+\frac{1}{2c}\int_{x-ct}^{x+ct} h(x') \,dx'+\\[3pt] \frac{1}{2c} \int_0^t \int_{x-c(t-t')}^{x+c(t-t')} f(x',t' )\,dx'd t' \label{equ-6.2} \end{multline}
Example. \begin{align*} &u_{tt}-4u_{xx}= \sin(x)\cos( t),\\ &u|_{t=0}= 0,\\ &u_t|_{t=0}= 0. \end{align*} Then $c=2$ and according to (\ref{equ-6.2}) \begin{multline*} u(x,t)= \frac{1}{4} \int_0^t \int_{x-2(t-t')}^{x+2(t-t')} \sin (x')\cos( t')\,dx' d t'=\\ \frac{1}{4} \int_0^t \Bigl[\cos \bigl(x-2(t-t')\bigr)-\cos \bigl( x+2(t-t')\bigr) \Bigr] \cos( t')\, d t'= \\ \frac{1}{2} \int_0^t \sin(x) \sin (2(t-t'))\cos( t')\, d t'=\\ \frac{1}{4}\sin(x) \int_0^t [\sin (2(t-t')+t')+\sin( 2(t-t')-t')]\, d t'=\\ \frac{1}{4}\sin(x) \int_0^t [\sin (2t-t')+\sin( 2t-3t')]\, d t'=\\ \frac{1}{4}\sin(x) \bigl[\cos (2t-t')+\frac{1}{3}\cos( 2t-3t')\bigr]_{t'=0}^{t'=t}=\\ \frac{1}{3}\sin(x)\bigl[\cos(t)-\cos(2t) \bigr]. \end{multline*} Sure, separation of variables would be simpler here.