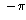 to
to 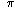 , and the sum of two numbers in this range is not
necessarily also in that range.
, and the sum of two numbers in this range is not
necessarily also in that range.
This is false. The principal argument always has to be in the range from
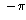 to
to 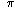 , and the sum of two numbers in this range is not
necessarily also in that range.
, and the sum of two numbers in this range is not
necessarily also in that range.
Question 1(b)
This is false. In fact, if we write z=x+iy and w=u+iv, then (x+iy)(u+iv) = (xu-yv) + i(xv+yu), so we see that the real part Re(zw) equals xu-yv = Re(z)Re(w) - Im(z)Im(w). This will not in general be equal to Re(z)Re(w), unless the product Im(z)Im(w) happens to be zero.
Question 1(c)
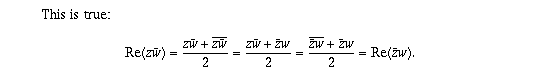
Question 1(d)
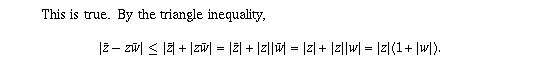
Question 1(e)
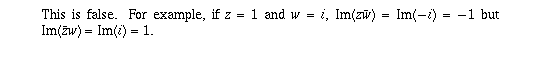
Question 2

Question 3(a)
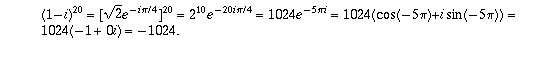
Question 3(b)

Question 4
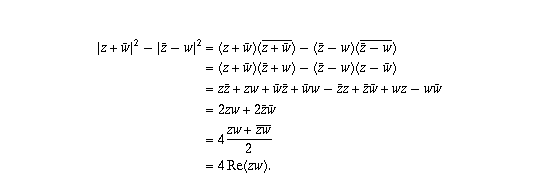
Question 5
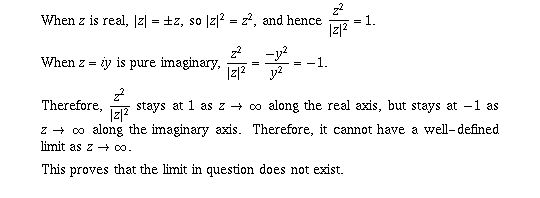
Question 6
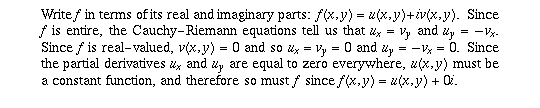
Question 7(a)

Question 7(b)
In order for f to be analytic at a point z, it must be differentiable on some disk centred at z. But we know f is differentiable only on a single line. There is no disk (of non-zero radius) that can be completely contained within that line. Therefore, there is no disk on which f is differentiable, and hence there is no point at which f is analytic.
![]() Go backward to Assignment 10 Solutions: Part 1
Go backward to Assignment 10 Solutions: Part 1![]() Go up to Contents
Go up to Contents![]() Go forward to Midterm 2 Solutions
Go forward to Midterm 2 Solutions![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)