(These buttons explained below)
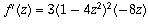
The differentiation formulas for sums, differences, products, quotients, integral powers, and composite functions are the same as for real-variable calculus, so these derivatives are the same as they would be for real-variable calculus.
(a) f'(z) = 6z - 2
(b)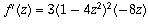 
(c)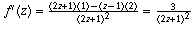 
(d)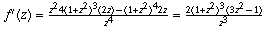 
Page 47 #2
(a) This follows immediately from the theorems on derivatives of integer powers, sums, and products.
(b)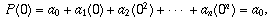 
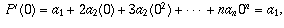and so on. (A rigorous proof would require induction, but I won't write out
all the details.)
Page 48 #7 (6th edition: #9)
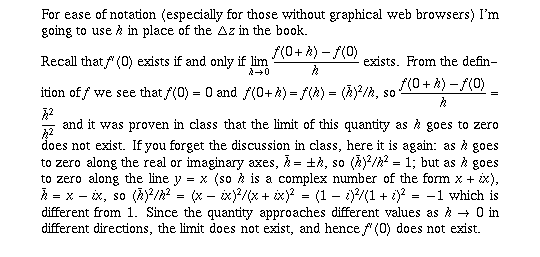
Page 48 #8(b,c)
These are done in the same manner as part (a) (which was done in class).
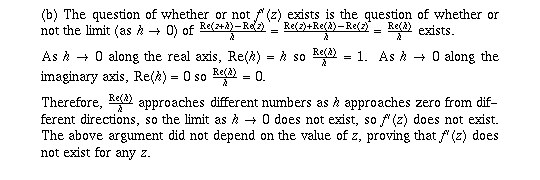
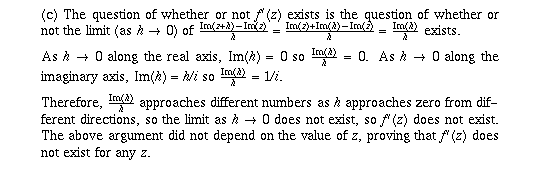
Page 54 #1
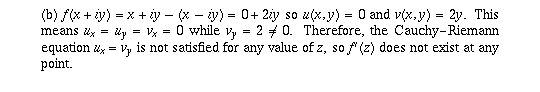
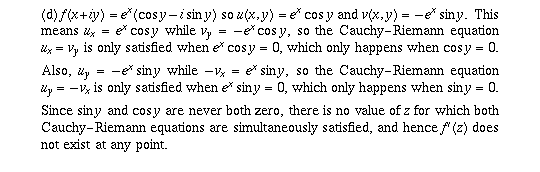
Page 54 #2
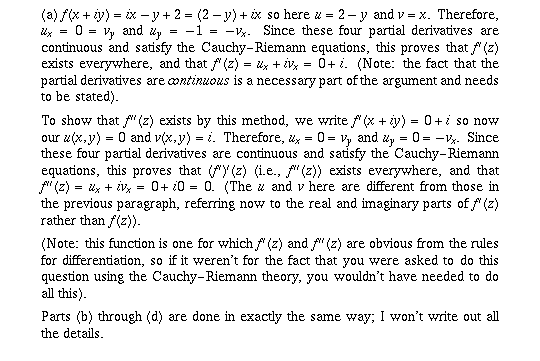
Page 54 #3
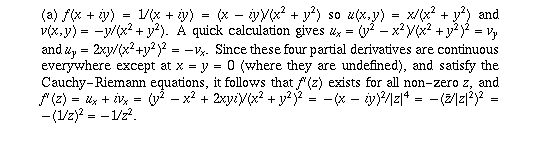
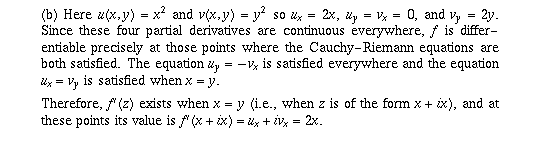
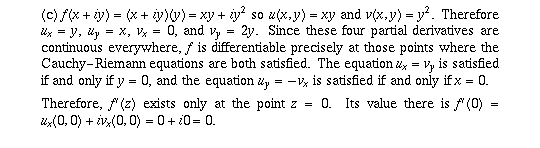
Page 54 #5
Page 54 #6
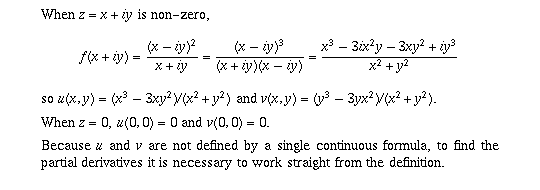
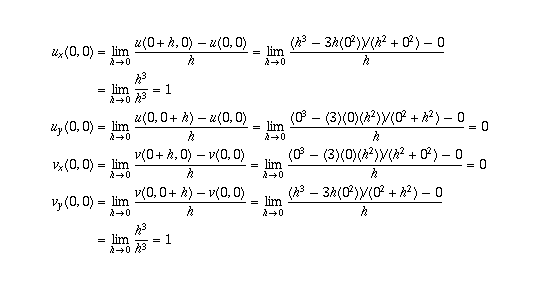
so, at z=0, the Cauchy-Riemann equations are satisfied:
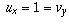and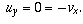 
Page 60 #1
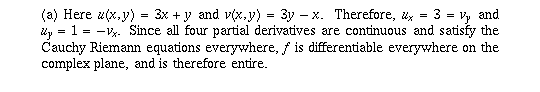
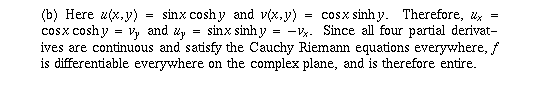
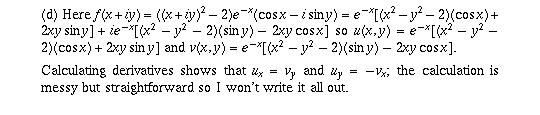
Since all four partial derivatives are continuous and satisfy the Cauchy Riemann equations everywhere, f is differentiable everywhere on the complex plane, and is therefore entire.
Note that this is not the best way of showing f is entire! The
best way is to write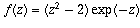 
and use the fact that
composites, sums, and products of entire functions are entire.
Page 60 #2
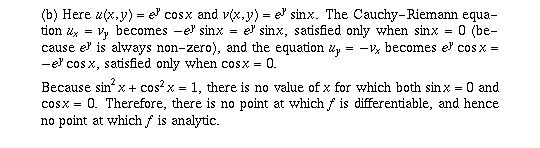
Page 60 #4
These are all combinations of polynomials. Polynomials are entire functions (differentiable everywhere). Sums, differences, and products of differentiable functions are entire. Quotients of differentiable functions are differentiable except where the denominator is zero.
Therefore, each of these functions are differentiable except at points where the denominator is zero. In each of these examples, these are just finitely many points (as given in the answers in the book). These are the singular points. The set of complex numbers other than these finitely many exceptions is an open set; f is differentiable everywhere on that open set; therefore, f is analytic everywhere on that open set.
Page 61 #7
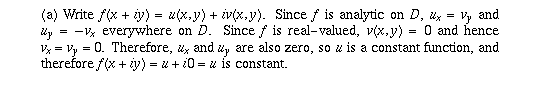
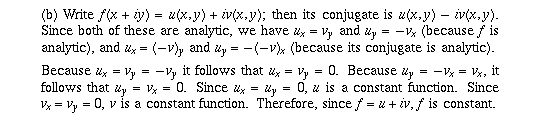
Page 61 #8 (6th edition: page 63 #10)
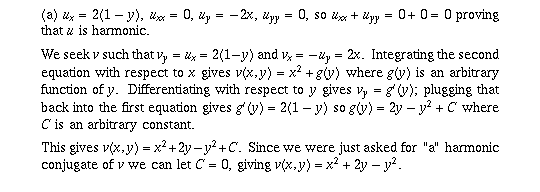
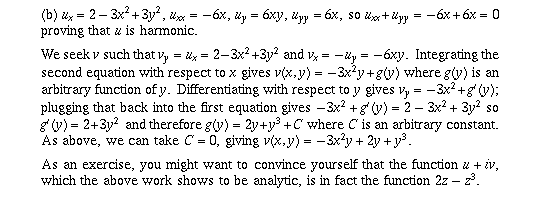
Page 61 #9 (6th edition: page 63 #11)
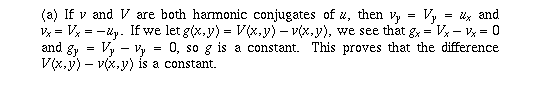
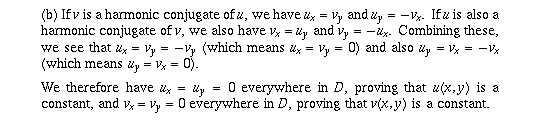
Go backward to Assignment 4 (due Thursday October 9th) Go up to Contents Go forward to Assignment 5 (due Thursday October 23rd) Switch to text-only version (no graphics)