Navigation Panel: 







 (These buttons explained below)
(These buttons explained below)
Assignment 3 Solutions
Page 32 #1 (6th edition: page 31 #1)
The principal argument Arg is defined for all non-zero numbers.
Division is defined as long as the denominator is non-zero. The other
operations used in these formulas (addition, subtraction, multiplication,
conjugation, and the modulus function) are defined for all complex numbers.
Therefore, the domain of each function is the set of complex numbers
for which all denominators in the formula are non-zero and for which Arg is
applied only to non-zero numbers.
For (a), this is all numbers other than 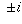 . For (b), this is
all non-zero numbers (note that 1/z is always non-zero so the
restriction on inputs to the Arg function having to be non-zero is
automatically satisfied). For (c), this is the set of
all numbers z for which
. For (b), this is
all non-zero numbers (note that 1/z is always non-zero so the
restriction on inputs to the Arg function having to be non-zero is
automatically satisfied). For (c), this is the set of
all numbers z for which
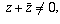 which is the same as saying
which is the same as saying 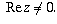 For (d), this is the set of all numbers z for which
For (d), this is the set of all numbers z for which 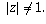
Page 32 #2 (6th edition: page 31 #2)
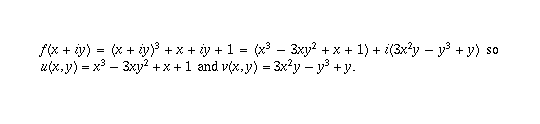
Page 32 #3 (6th edition: page 31 #3)
Just plug the given expressions for x and y into the formula
for f(z) and simplify (and use the fact that 1/i = -i). It's
straightforward algebra so I won't write it all out.
Page 32 #4 (6th edition: page 33 #13)
(a) The sector 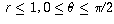
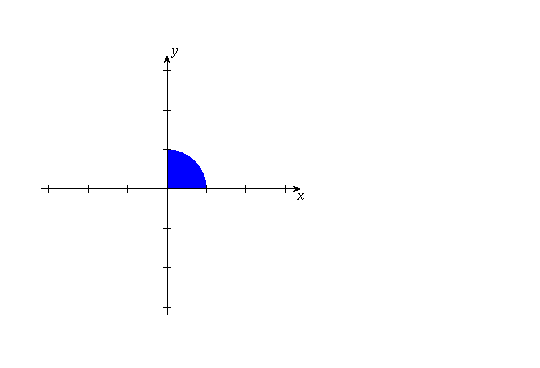
(b) The sector 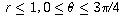
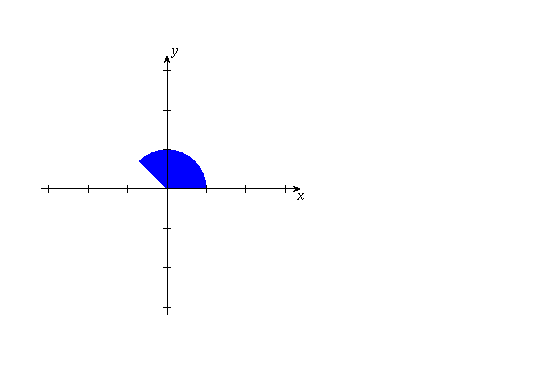
(c) The sector 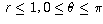
Page 32 #6 (6th edition: page 32 #12)
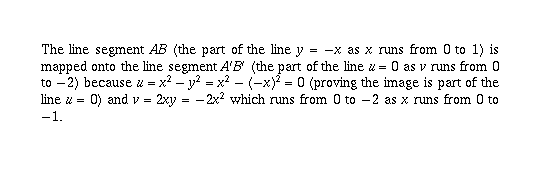
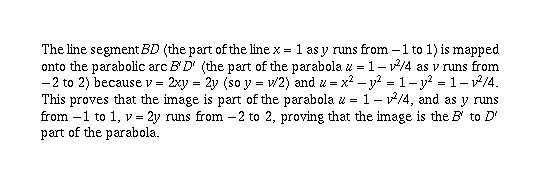
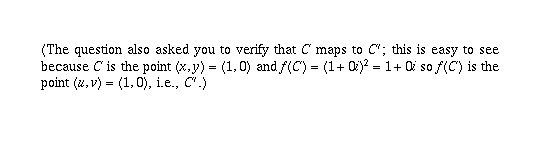
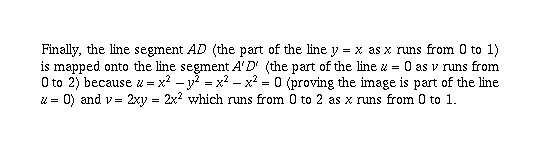
This proves the boundary of the indicated region in the x,y plane
maps to the boundary of the indicated region in the u,v plane.
You could also construct a rigorous argument that points inside the
boundary get mapped to points inside, and points outside get mapped to
points outside, but it's a bit of a pain to do it precisely using the
machinery at our disposal so far, so don't bother.
Page 33 #10 (6th edition: page 33 #14)
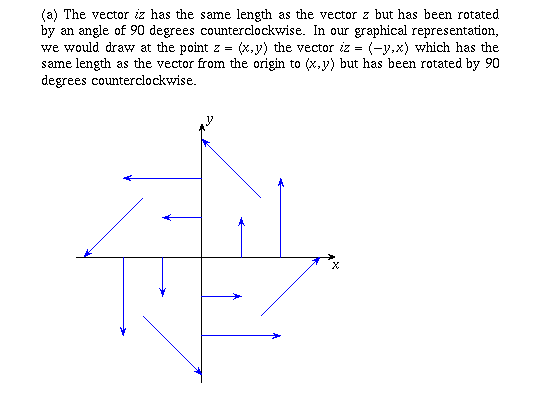
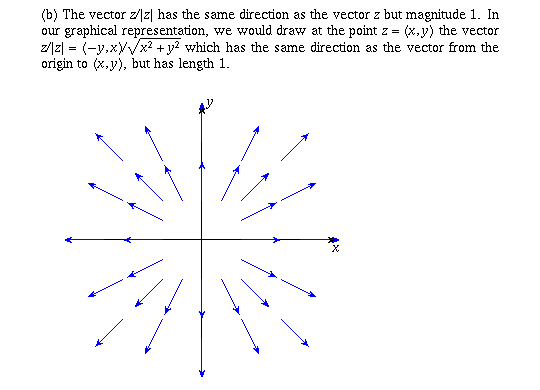
Page 42 #3 (6th edition: #2)
Recall the basic theorems on limits of sums, products, quotients,
compositions, and that
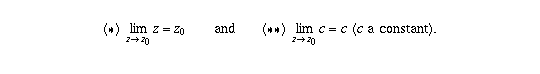
From these we can prove by induction that
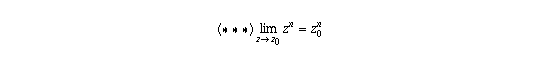
for all integers n (this was done in class).
From this, the theorem on the limits of quotients, and the assumption
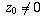 , it follows that the limit in part (a) equals
, it follows that the limit in part (a) equals
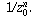
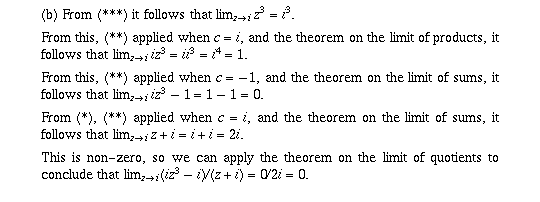

The only time when you would write out such full and pedantic
justifications of these limit formulas is in an exercise such as this.
Normally you would just write down the answer (which you can see by
inspection). Other than an in an exercise like this, you would not need to show
any of the intermediate steps,
except that you do need to show the denominator is non-zero when using
the theorem on quotients.
Page 42 #5 (6th edition: #7)

Page 42 #8 (6th edition: #9)
Let me write out the three key properties of limits involving infinity, so I
can refer to them in a uniform way without worrying about the fact that they
have different equation numbers in different editions of the textbook:
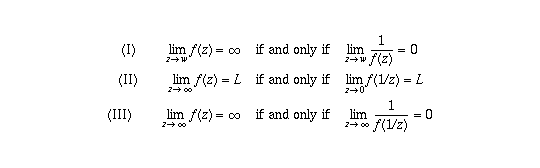
(a) Because of property (II) this follows by showing
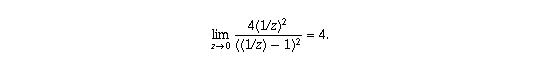
This in turn follows from
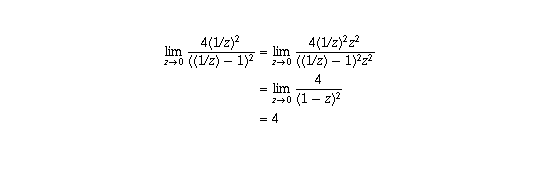
using part (c) of exercise 3 (exercise 2 in the 6th edition).
(b) Because of property (I) this follows by showing
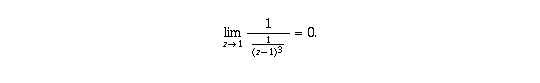
This in turn follows from
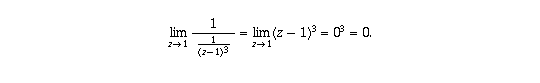
(c) Because of property (III) this follows by showing
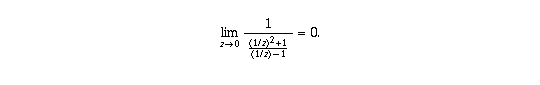
This in turn follows from
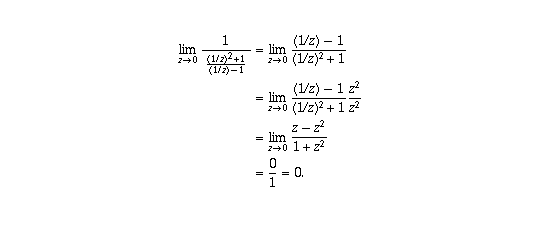
Page 43 #9 (6th edition: #10)
(a) Because of property (III) this follows from
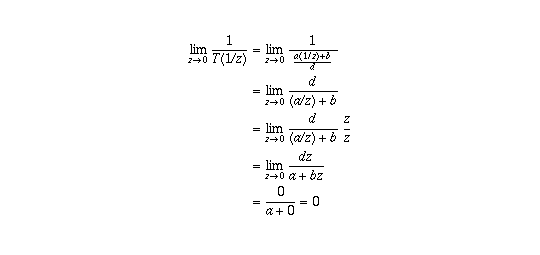
where the last line follows from the limits on quotients together with the
fact that, when c=0, the assumption 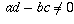 guarantees that
a is non-zero. (Without this assumption the numerator and denominator would
both be zero and the result would not hold. In fact, in this case T(z) would
be the constant function b/d so its limit would be b/d not infinity.)
guarantees that
a is non-zero. (Without this assumption the numerator and denominator would
both be zero and the result would not hold. In fact, in this case T(z) would
be the constant function b/d so its limit would be b/d not infinity.)
(b) Because of property (II) the first statement follows from
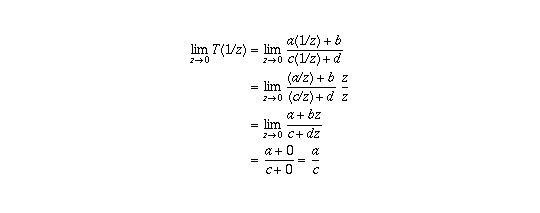
where the last line follows from the limits on quotients together with the
assumption that c is non-zero.
Because of property (I), the second statement follows from
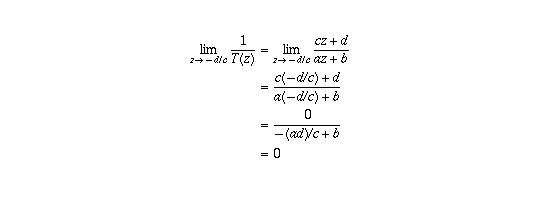
where the second line follows from part (c) of exercise 3 (exercise 2 in the
6th edition), together with the fact that the denominator equals
(-1/c)(ad-bc) which is well-defined and non-zero because of our
assumptions that c and ad-bc are each non-zero.
Page 43 #13 (6th edition: #14)
S is unbounded if and only if there is no real number M with the property
that
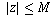 for every
for every 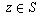 .
.
This is true if and only if, for each
positive real number M, there is at least
one 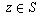 for which
for which 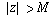 .
.
Letting 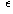 denote 1/M, we see that this is true if and only if,
for each positive real number
denote 1/M, we see that this is true if and only if,
for each positive real number 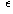 , there is at least one
, there is at least one
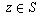 for which
for which 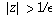 .
.
This is the same as saying that, for each 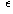 -neighbourhood of infinity,
there is at least one
-neighbourhood of infinity,
there is at least one 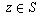 for which z belongs to that
neighbourhood.
for which z belongs to that
neighbourhood.
This is the same as saying that every neigbourhood of infinity contains at
least one point of S.
Navigation Panel: 








 Go backward to Assignment 3 (due Thursday October 2nd)
Go backward to Assignment 3 (due Thursday October 2nd)
 Go up to Contents
Go up to Contents
 Go forward to Assignment 4 (due Thursday October 9th)
Go forward to Assignment 4 (due Thursday October 9th)
 Switch to text-only version (no graphics)
Switch to text-only version (no graphics)
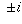 . For (b), this is
all non-zero numbers (note that 1/z is always non-zero so the
restriction on inputs to the Arg function having to be non-zero is
automatically satisfied). For (c), this is the set of
all numbers z for which
. For (b), this is
all non-zero numbers (note that 1/z is always non-zero so the
restriction on inputs to the Arg function having to be non-zero is
automatically satisfied). For (c), this is the set of
all numbers z for which
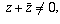 which is the same as saying
which is the same as saying 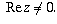 For (d), this is the set of all numbers z for which
For (d), this is the set of all numbers z for which 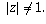
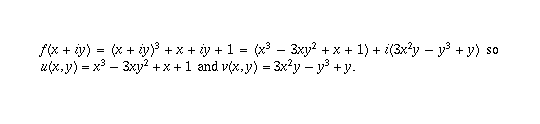
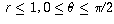
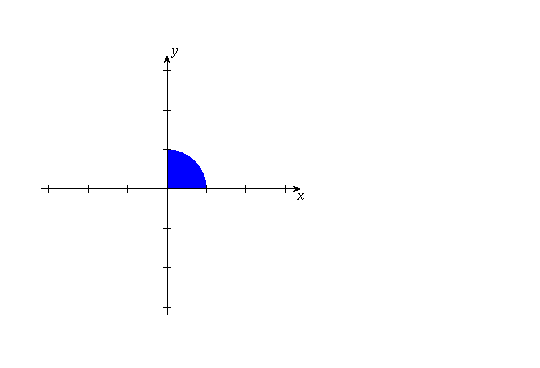
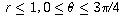


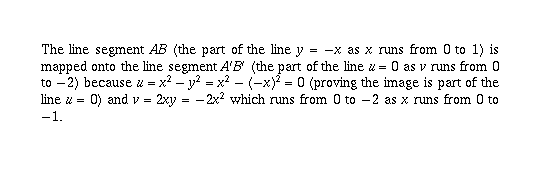
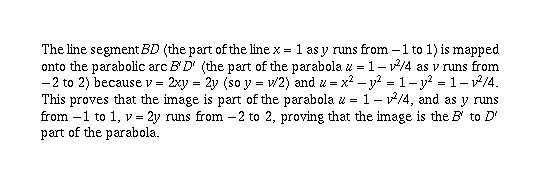
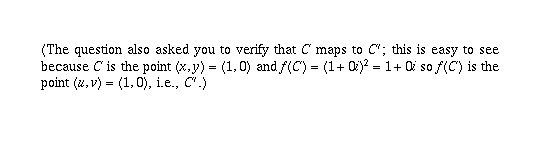
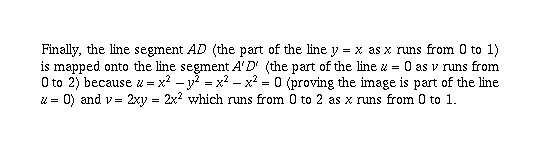


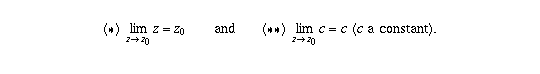
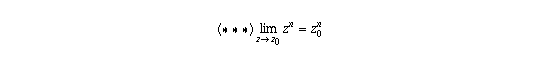
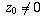 , it follows that the limit in part (a) equals
, it follows that the limit in part (a) equals
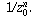
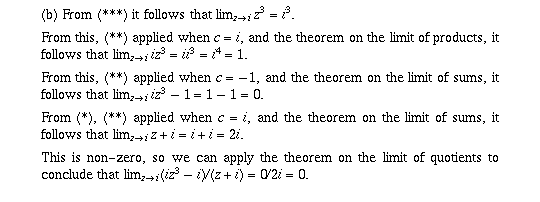


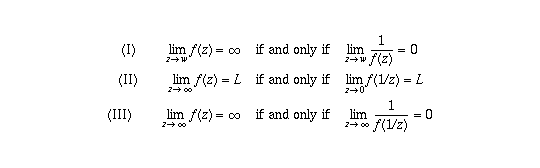
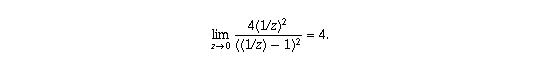
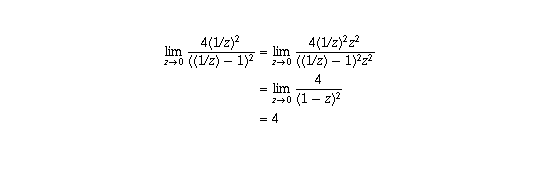
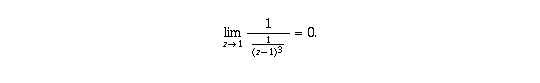
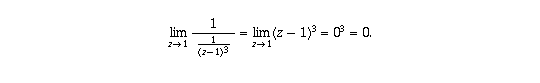
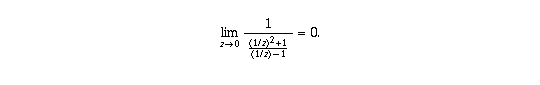
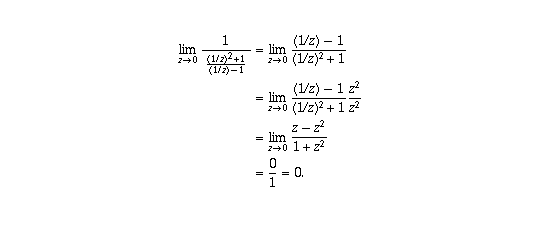
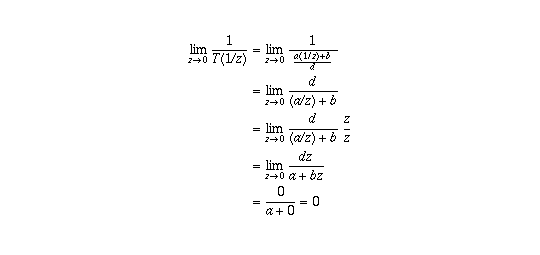
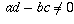 guarantees that
a is non-zero. (Without this assumption the numerator and denominator would
both be zero and the result would not hold. In fact, in this case T(z) would
be the constant function b/d so its limit would be b/d not infinity.)
guarantees that
a is non-zero. (Without this assumption the numerator and denominator would
both be zero and the result would not hold. In fact, in this case T(z) would
be the constant function b/d so its limit would be b/d not infinity.)
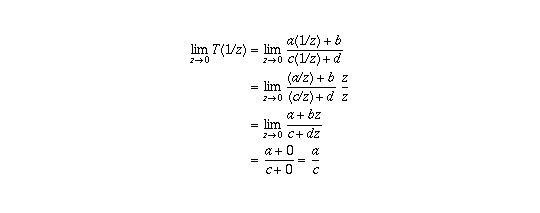
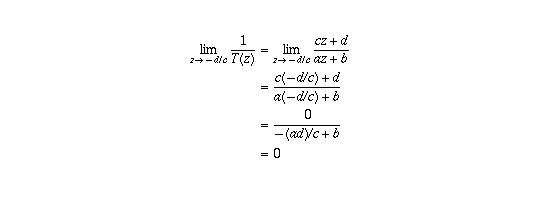
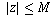 for every
for every 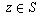 .
.
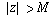 .
.
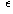 denote 1/M, we see that this is true if and only if,
for each positive real number
denote 1/M, we see that this is true if and only if,
for each positive real number 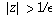 .
.