(These buttons explained below)
Page 20 #2 (6th edition: Page 17 #2)
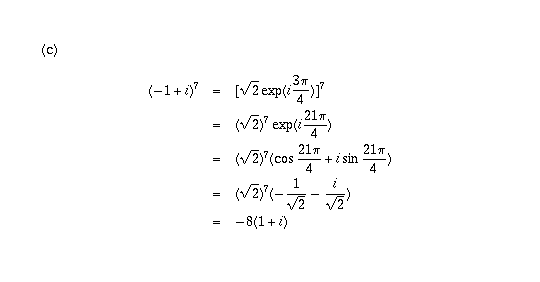
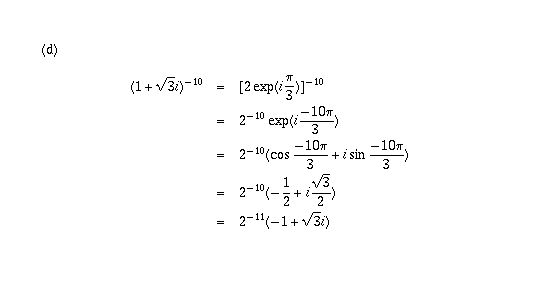
Page 21 #3(c-f) (6th edition: Page 22 #2(a-d))
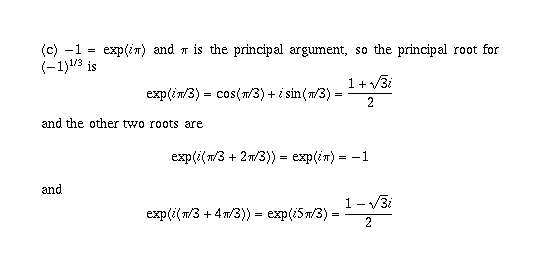
(e) and (f) are done similarly and the answers are in the book, so I won't
write them out. The principal root for (e) is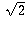 
and the principal
root for (f) is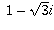 
. This may be worth going over:
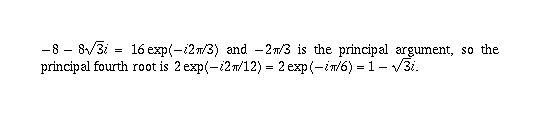
Page 21 #5 (6th edition: Page 17 #4)
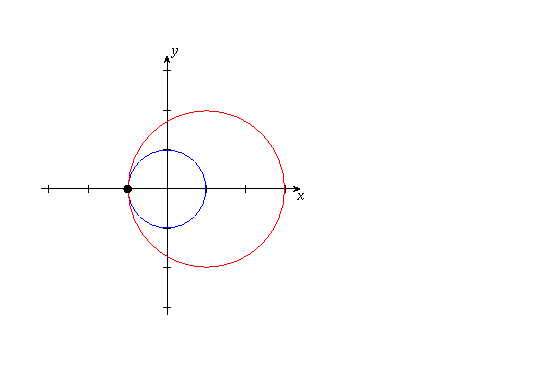
The equation is equivalent to
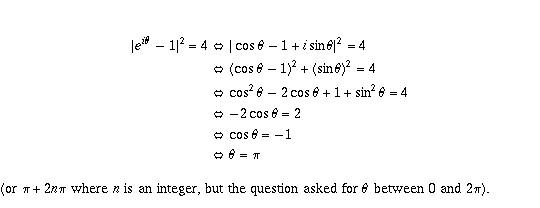
This can also be seen geometrically: numbers of the form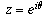 
are those that lie on the unit circle |z|=1, while
those that satisfy the equation |z-1|=2 are those on the circle of radius 2
centred at 1. Therefore, the desired number 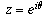must be on both those circles. The circles intersect
only at the complex number -1 (the point (-1,0)), where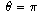 
.
Page 21 #8 (6th edition: page 17 #6)
Page 22 #12 (6th edition: page 22 #4)
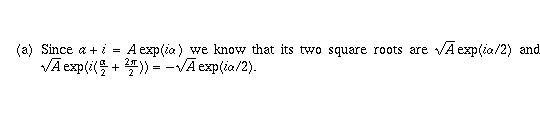
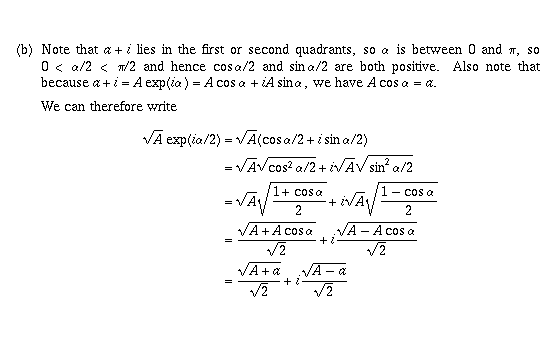
Page 22 #13 (6th edition: page 22 #5)
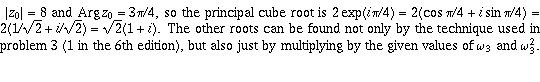
Page 22 #14 (6th edition: page 22 #6)
The desired roots are the fourth roots of -4. These are found just as in
problem 3c (2a in the 6th edition) to be 1+i, -1+i, -1-i, and 1-i.
This means the polynomial factors as [z-(1+i)][z-(-1+i)][z-(-1-i)][z-(1-i)]
= (z-1-i)(z+1-i)(z+1+i)(z-1+i). The product of the first and fourth factors
is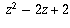 
while the product of the second and third factors is
.
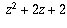Page 22 #15 (6th edition: page 17 #9)
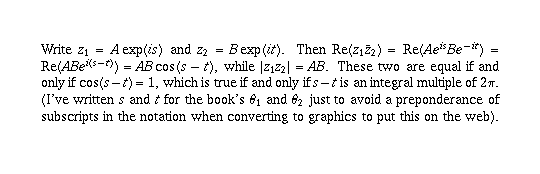
Page 22 #16(a) (6th edition: page 17 #10)
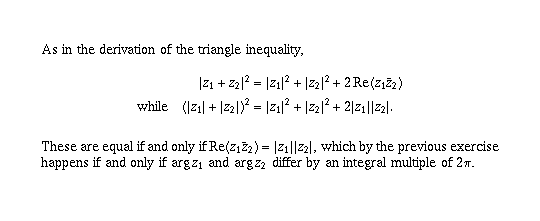
Geometrically, this happens if and only if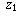 
and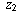 
are vectors that
point in the same direction; in all other cases it is clear that the third side
of the triangle they form will be shorter than the sum of the first two sides.
Page 23 #19 (6th edition: page 22 #7)
Just plug in to the first identity of the previous question (using c in place of z and n-1 in place of n, together with the fact that c is not equal to 1 so it makes sense to divide by c-1).
Page 23 #21 (6th edition: page 18 #12)
Page 25 #1
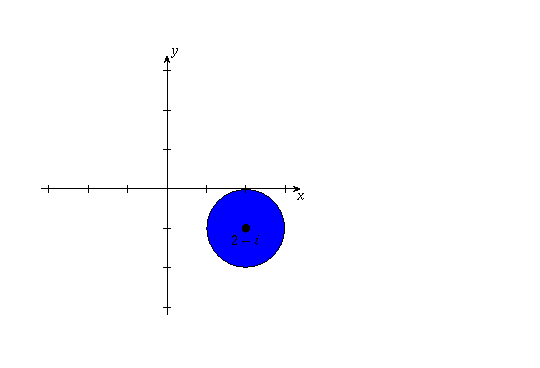
(a) This is a closed disk (circle together with the points inside the circle) of radius 1 centred at 2-i. There are boundary points (the points on the circle); these are all contained within the set, so the set is closed and is not open. Therefore, it is not a domain. It is, however, connected.
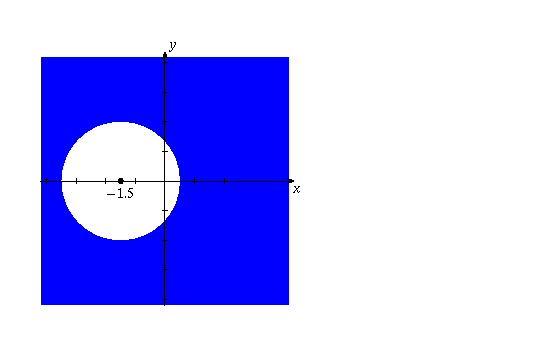
(b) This can be rewritten |z - (-3/2)| > 2. It is the set of points outside the circle of radius 2 centred at -3/2. There are boundary points (the points on the circle); none of these boundary points is included in the set, so the set is not closed and is open. It is also connected. Therefore, it is a domain.
(c) This is the set of points above the line y=1. There are boundary points (the points on the line); none of these boundary points is included in the set, so the set is not closed and is open. It is also connected. Therefore, it is a domain.
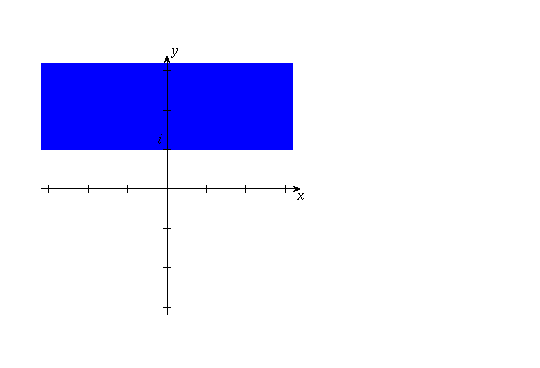
(d) This is the line y=1. There are boundary points; in fact, the set of boundary points is the set itself. (To understand why every point on the line is a boundary point, note that if you take any neighbourhood of a point on the line, that neighbourhood will stick out above and below the line so it will contain both points in the set and points not in the set). Since all the boundary points are included in the set, the set is closed and is not open. Therefore, it is not a domain. (However, it is connected).
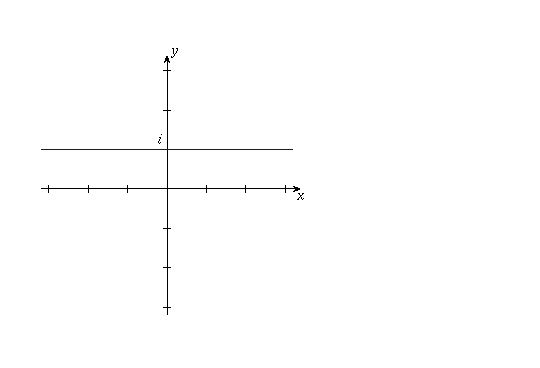
(e) This is the wedge consisting of all first-quadrant points that lie
on or below the line y=x and on or above the x-axis, except for the origin.
There are boundary points; points where arg z is 0 or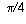 
are boundary points (and these are included in the set), and the origin is also
a boundary point (which is not included in the set). Since the set contains
some but not all of its boundary points, it is neither open nor closed. It is
therefore not a domain. (It is, however, connected).
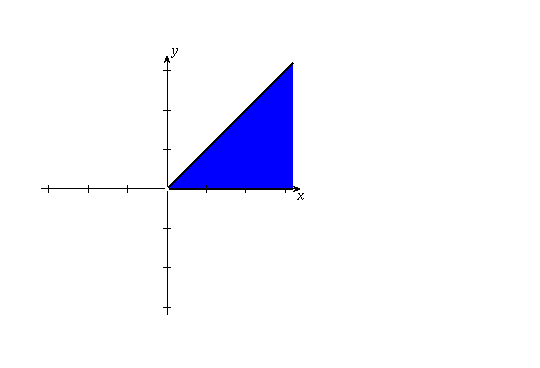
(f) This is the set of points which are closer to or the same distance from the origin as they are to 4; in other words, the set of points on or to the left of the line x=2. This set has boundary points (points on the line are boundary points); these are all included in the set, so the set is closed and not open. It is therefore not a domain. (It is, however, connected).
Page 25 #2
See the answers to question 1.
Page 25 #3
(a) is the only bounded set.
Page 25 #5
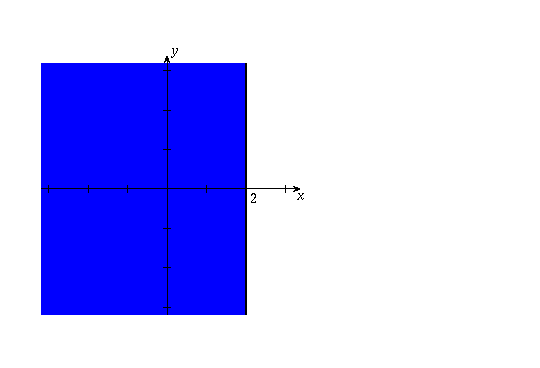
S is not connected because if you take a point z in the |z|<1 portion of the set and a point w in the point |w-2|<1 portion of the set, you cannot draw a path from z to w without going outside the set.
(However, note that if the point 1 were part of the set, then you could get from z to w by a path that stays inside the set).
Go backward to Assignment 2 (due Tuesday September 30th) Go up to Contents Go forward to Assignment 3 (due Thursday October 2nd) Switch to text-only version (no graphics)