(These buttons explained below)
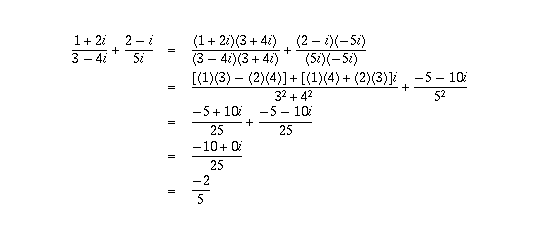
These are straightforward applications of the formulas for sums, differences, products, and quotients. I won't write them all out. Here is part (d) as an example:
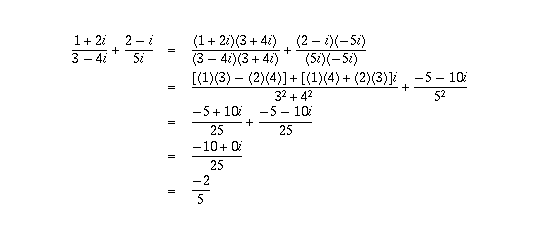
Page 5 #4 (6th edition: #12)
Page 6 #6 (6th edition: #8(a))
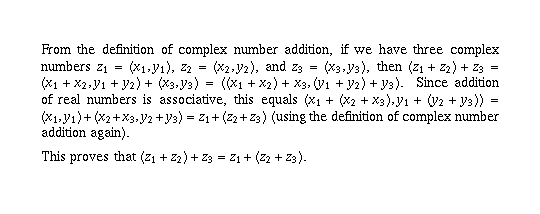
Page 6 #10 (6th edition: #4)
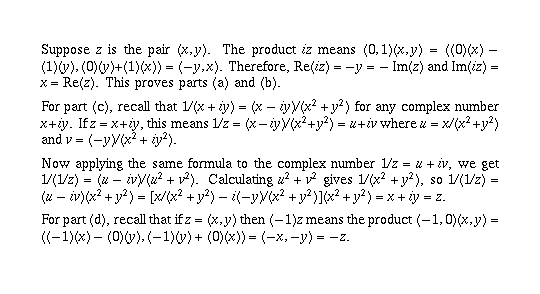
Page 6 #15 (6th edition: #14)
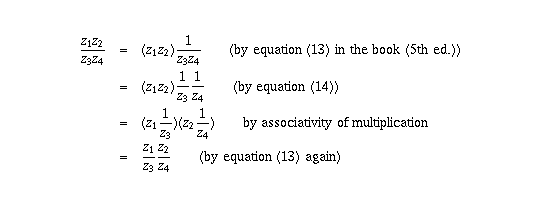
The cancellation law follows from this by writing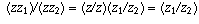 
.
Page 11 #1
For part (a):
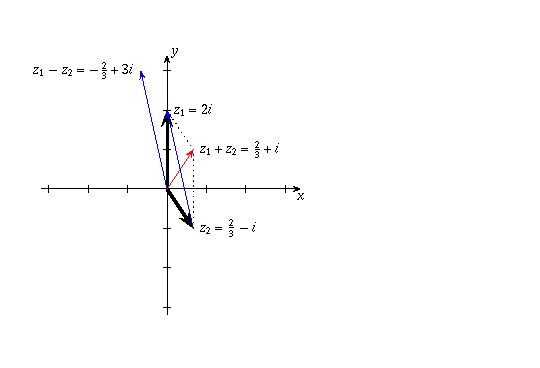
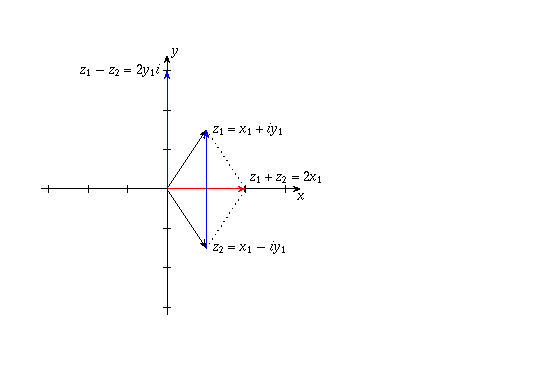
The other parts are similar. Note that for part (d), even though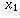 
and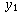 
are unspecified, you know that 
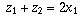is purely real
(hence a horizontal vector) and 
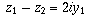is purely imaginary
(hence a horizontal vector). In the case where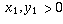 
, the
picture looks as follows:
Page 11 #2
Part (a) follows because
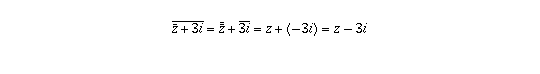
(the first inequality is from the law
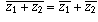, the second from the
law that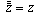 
(and the fact that the conjugate of 3i=0+3i is
0-3i, i.e. -3i).
Parts (b) and (c) are similar; I won't write them all out.
Part (d) follows because
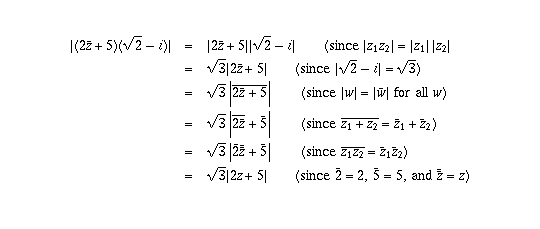
Page 11 #4
First we prove that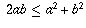 
for all real numbers
a and b. We do this by observing that
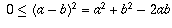and the desired inequality follows by
adding 2ab to each side.
Now,
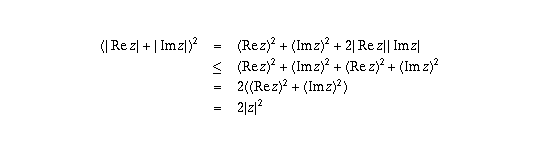
Since both | Re z| + |Im z |
and | z | are non-negative, it is legitimate to
take the square roots of both sides to conclude that
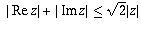, as desired. (For non-negative
numbers A and B,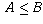 
if and only if 
).
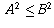Page 11 #6 (6th edition: #14)
For part (a), note that z is real if and only if Im z = 0, i.e.,
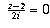, which is true if and only if
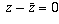(i.e., 
).
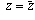For part (b): if z is either real or pure imaginary, then either
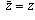or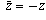 
, and in either case
.
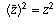Conversely, if 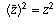, then
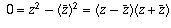, so either
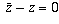or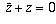 
, so either
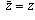or ,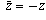
so z is either real or pure imaginary.
Page 11 #10 (6th edition: #9)
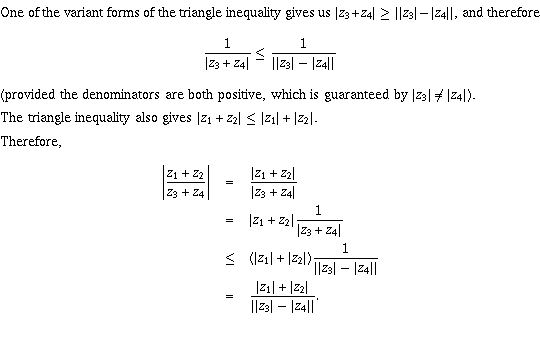
Page 11 #11 (6th edition: #10)
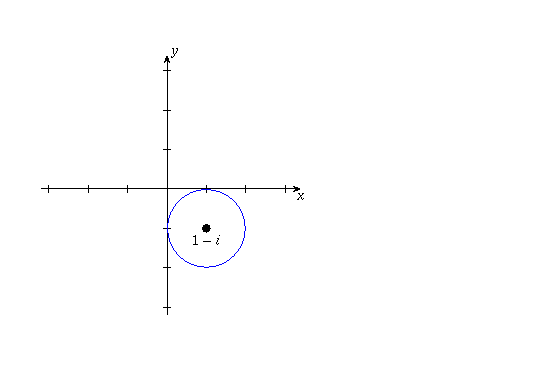
(a) Circle of radius 1 centred at 1-i.
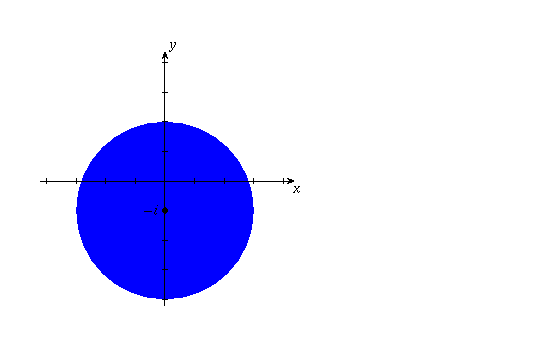
(b) Closed disk (circle together with the points inside the circle) of radius 3 centred at -i.
(c) If z=x+iy,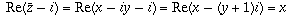 
so the sketch consists of the line x=2.
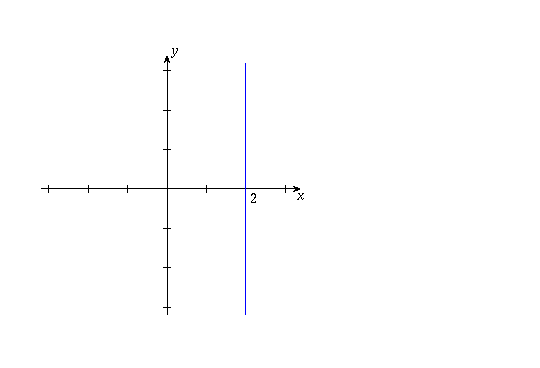
(d) Since |2z-i|=4 is equivalent to |z-(1/2)i| = 2, the sketch is a circle of radius 2 centred at 0.5i.
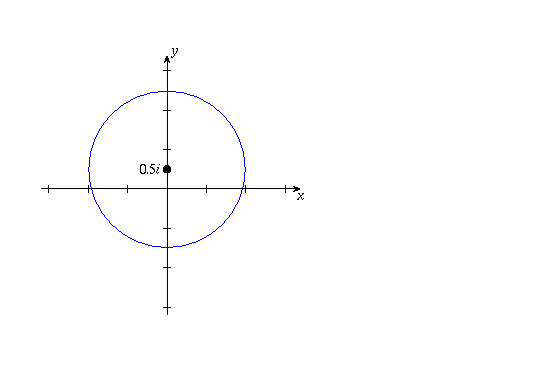
Page 11 #13 (6th edition: #12)
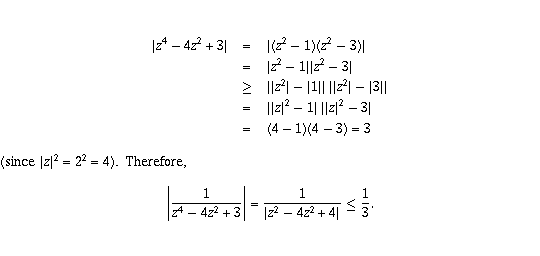
Page 12 #17
Since two non-negative numbers are equal if and only if their squares are equal, the equation can be rewritten
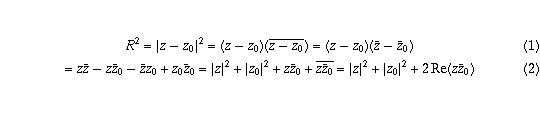
Page 12 #18
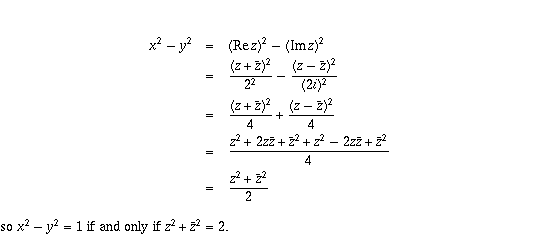
Page 12 #19
(a) This equation represents the set of points for which the sum of the distance to 4i (i.e., the point (0,4)) and the distance to -4i (i.e., the point (0,-4)) is 10. Geometrically, the set of points for which the sum of the distance to point P and the distance to point Q is a fixed value is an ellipse with foci at P and Q.
(b) This equation represents the set of points that are equidistant from 1 (i.e., the point (1,0)) and -i (i.e., the point (0,-1)). This set is the line bisecting the line segment joining these two points, which is the line through the origin with slope -1.
Go backward to Assignment 1 (due Tuesday September 23rd) Go up to Contents Go forward to Assignment 2 (due Tuesday September 30th) Switch to text-only version (no graphics)