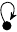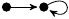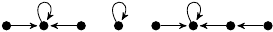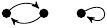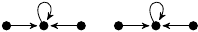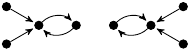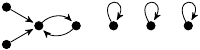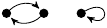Preperiodic Point Portraits of Cubic Polynomials
This page tabulates the results of a 2013 USRA project that I undertook with the supervision of Kevin Hare and David McKinnon at the University of Waterloo. The goal of the project was to explore the possible directed graph structures of the set of rational preperiodic points of cubic polynomials defined over Q. Using the data from the 2007 Small Height Points for Cubic Polynomials REU project by Rob Benedetto and his students, and by writing a Python program to classify finite functional digraphs by isomorphism, I found there to be exactly 103 distinct preperiodic point portraits exhibited among the first 14 billion conjugacy classes of cubic polynomials ordered by naïve height. My old writeup (from 2013) is available here.
The portraits on this page are grouped into two tables, one for each of Benedetto et al.’s two “normal forms” for cubic polynomials:
az3 + bz + 1 and az3 + bz.
Every cubic polynomial over Q is linearly conjugate (viz. via some z ↦ αz + β) to one in normal form (cf. §4 of their paper). Since conjugacy induces an isomorphism between associated functional digraphs, the preperiodic point portrait of a cubic polynomial depends only on its normal form.
The portraits are depicted as unlabelled directed graphs (hand-coded in TikZ). Each portrait Γ is accompanied by a listing of several statistics, namely:
- #
- a unique ordinal number
- N
- the number of instances of Γ among the polynomials in the data, with a link to a text file listing them. The files are formatted in the same manner as Benedetto’s, and the entries contain the same information (see Reading the data files). Note that the files for the trivial portraits I1 and II3 list only those polynomials with at least one nontrivial point of small canonical height.
- f(z)
- a representative of least height. In the (rare) cases where there does not exist a representative that minimizes the naïve height and the moduli height simultaneously, two representatives are given (cf. portraits 36, 38, 55, 68, 69, and 78 in Table 1).
- H
- the least naïve height of a representative, defined as max {H(a), H(b)}
- H*
- the least moduli height of a representative, defined as H(a : b : 1) for the first normal form and as H(b) for the second. This statistic is omitted from Table 2 because H* = H in each case there.
- p
- the number of vertices/edges (= “number of preperiodic points”)
- c
- the length of the longest directed path (= “maximum length of a preperiodic chain”)
- l
- the length of the biggest cycle (= “maximum length of a periodic cycle”)
- k
- the number of connected components
- cycles
- a list of all cycle lengths, repeated according to multiplicity
- degree
- a 4-tuple (d0, d1, d2, d3) where di counts the number of vertices with in-degree equal to i
- structure
- zero or more lines of the form “nm: an,0, an,1, an,2, …” where an,m counts the number of vertices that are m edges away from an n-cycle
There are 79 portraits in Table 1 and 37 portraits in Table 2. The two tables have 13 portraits in common: portraits 1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 17, 29, and 33 in Table 2 are isomorphic to portraits 29, 30, 3, 4, 40, 14, 44, 53, 49, 43, 70, 66, and 33 in Table 1, respectively.
The tables can be sorted ascending or descending by clicking on the column headers.
az3 + bz + 1
Table 1. Preperiodic point portraits of polynomials of the form az3 + bz + 1 with H(a) and H(b) less than 300
| # |
Γ |
N |
f(z) |
H |
H* |
p |
c |
l |
k |
cycles |
degree |
structure |
| 1. |
 |
11,939,559,973 (21 MB) |
z3 + 1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
(0, 0, 0, 0) |
|
| 2. |
 |
84,404 (3 MB) |
−z3 + 1 |
1 |
1 |
2 |
2 |
2 |
1 |
2 |
(0, 2, 0, 0) |
2m: 2 |
| 3. |
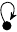 |
282,083 (12 MB) |
z3 + z + 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
(0, 1, 0, 0) |
1m: 1 |
| 4. |
 |
112,291 (6 MB) |
z3 − z + 1 |
1 |
1 |
3 |
2 |
1 |
1 |
1 |
(2, 0, 0, 1) |
1m: 1, 2 |
| 5. |
 |
5 (351 B) |
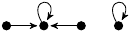
z3/2 − z/2 + 1 |
2 |
2 |
4 |
2 |
1 |
2 |
1, 1 |
(2, 1, 0, 1) |
1m: 2, 2 |
| 6. |
 |
1,003 (78 kB) |
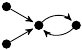
−2z3 + z/2 + 1 |
2 |
4 |
4 |
3 |
2 |
1 |
2 |
(2, 1, 0, 1) |
2m: 2, 2 |
| 7. |
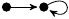 |
91 (5 kB) |
−z3 + 3z + 1 |
3 |
3 |
2 |
2 |
1 |
1 |
1 |
(1, 0, 1, 0) |
1m: 1, 1 |
| 8. |
 |
2 (149 B) |
z3/2 − 3z/2 + 1 |
3 |
3 |
5 |
3 |
2 |
2 |
1, 2 |
(2, 1, 2, 0) |
1m: 1, 1
2m: 2, 1 |
| 9. |
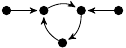 |
1 (67 B) |
−z3/2 + 3z/2 + 1 |
3 |
3 |
5 |
4 |
3 |
1 |
3 |
(2, 1, 2, 0) |
3m: 3, 2 |
| 10. |
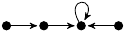 |
277 (24 kB) |
z3/3 − z/3 + 1 |
3 |
3 |
4 |
3 |
1 |
1 |
1 |
(2, 1, 0, 1) |
1m: 1, 2, 1 |
| 11. |
 |
42 (2 kB) |
4z3 − 2z + 1 |
4 |
4 |
2 |
1 |
1 |
2 |
1, 1 |
(0, 2, 0, 0) |
1m: 2 |
| 12. |
 |
7 (420 B) |
−4z3 + 3z + 1 |
4 |
4 |
3 |
3 |
2 |
1 |
2 |
(1, 1, 1, 0) |
2m: 2, 1 |
| 13. |
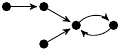 |
57 (5 kB) |
z3/3 − 4z/3 + 1 |
4 |
4 |
5 |
4 |
2 |
1 |
2 |
(2, 2, 0, 1) |
2m: 2, 2, 1 |
| 14. |
 |
274 (25 kB) |
4z3/3 − 4z/3 + 1 |
4 |
4 |
5 |
2 |
1 |
3 |
1, 1, 1 |
(2, 2, 0, 1) |
1m: 3, 2 |
| 15. |
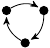 |
80 (6 kB) |
−z3 + 5z/4 + 1 |
5 |
5 |
3 |
3 |
3 |
1 |
3 |
(0, 3, 0, 0) |
3m: 3 |
| 16. |
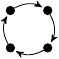 |
7 (552 B) |
−2z3/3 + 5z/3 + 1 |
5 |
5 |
4 |
4 |
4 |
1 |
4 |
(0, 4, 0, 0) |
4m: 4 |
| 17. |
 |
29 (3 kB) |
z3/6 − z/6 + 1 |
6 |
6 |
6 |
3 |
1 |
3 |
1, 1, 1 |
(2, 3, 0, 1) |
1m: 3, 2, 1 |
| 18. |
 |
14 (1 kB) |
−z3/6 + z/6 + 1 |
6 |
6 |
5 |
4 |
1 |
1 |
1 |
(2, 2, 0, 1) |
1m: 1, 2, 1, 1 |
| 19. |
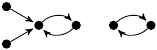 |
12 (1 kB) |
−2z3/3 + z/6 + 1 |
6 |
6 |
6 |
3 |
2 |
2 |
2, 2 |
(2, 3, 0, 1) |
2m: 4, 2 |
| 20. |
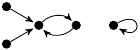 |
21 (2 kB) |
−3z3/2 + z/6 + 1 |
6 |
9 |
5 |
3 |
2 |
2 |
1, 2 |
(2, 2, 0, 1) |
1m: 1
2m: 2, 2 |
| 21. |
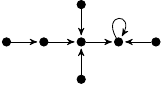 |
6 (595 B) |
z3/3 − 7z/3 + 1 |
7 |
7 |
7 |
4 |
1 |
1 |
1 |
(4, 1, 0, 2) |
1m: 1, 2, 3, 1 |
| 22. |
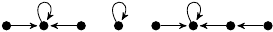 |
10 (1 kB) |
2z3/3 − 7z/6 + 1 |
7 |
7 |
8 |
3 |
1 |
3 |
1, 1, 1 |
(4, 2, 0, 2) |
1m: 3, 4, 1 |
| 23. |
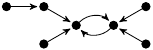 |
13 (1 kB) |
−2z3/3 + 7z/6 + 1 |
7 |
7 |
7 |
4 |
2 |
1 |
2 |
(4, 1, 0, 2) |
2m: 2, 4, 1 |
| 24. |
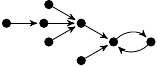 |
1 (112 B) |
−3z3/2 + 7z/6 + 1 |
7 |
9 |
8 |
5 |
2 |
1 |
2 |
(4, 2, 0, 2) |
2m: 2, 2, 3, 1 |
| 25. |
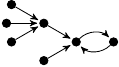 |
2 (201 B) |
z3/6 − 7z/6 + 1 |
7 |
7 |
7 |
4 |
2 |
1 |
2 |
(4, 1, 0, 2) |
2m: 2, 2, 3 |
| 26. |
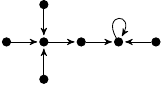 |
2 (182 B) |
−z3/6 + 7z/6 + 1 |
7 |
7 |
7 |
4 |
1 |
1 |
1 |
(4, 1, 0, 2) |
1m: 1, 2, 1, 3 |
| 27. |
 |
2 (115 B) |
3z3/2 − 9z/2 + 1 |
9 |
9 |
3 |
3 |
1 |
1 |
1 |
(1, 1, 1, 0) |
1m: 1, 1, 1 |
| 28. |
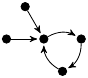 |
8 (1 kB) |
z3/4 − 9z/4 + 1 |
9 |
9 |
5 |
4 |
3 |
1 |
3 |
(2, 2, 0, 1) |
3m: 3, 2 |
| 29. |
 |
840 (59 kB) |
9z3/2 − 5z/2 + 1 |
9 |
9 |
3 |
1 |
1 |
3 |
1, 1, 1 |
(0, 3, 0, 0) |
1m: 3 |
| 30. |
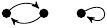 |
210 (12 kB) |
−9z3/10 − z/10 + 1 |
10 |
10 |
3 |
2 |
2 |
2 |
1, 2 |
(0, 3, 0, 0) |
1m: 1
2m: 2 |
| 31. |
 |
80 (5 kB) |
−9z3/10 + 11z/10 + 1 |
11 |
11 |
4 |
2 |
2 |
2 |
2, 2 |
(0, 4, 0, 0) |
2m: 4 |
| 32. |
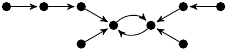 |
2 (216 B) |
z3/6 − 13z/6 + 1 |
13 |
13 |
9 |
5 |
2 |
1 |
2 |
(4, 3, 0, 2) |
2m: 2, 4, 2, 1 |
| 33. |
 |
1 (108 B) |
−z3/6 + 13z/6 + 1 |
13 |
13 |
9 |
3 |
1 |
3 |
1, 1, 1 |
(4, 3, 0, 2) |
1m: 3, 4, 2 |
| 34. |
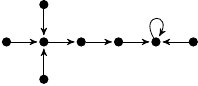 |
1 (106 B) |
2z3/3 − 13z/6 + 1 |
13 |
13 |
8 |
5 |
1 |
1 |
1 |
(4, 2, 0, 2) |
1m: 1, 2, 1, 1, 3 |
| 35. |
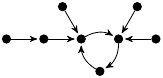 |
1 (110 B) |
−4z3/3 + 13z/12 + 1 |
13 |
16 |
8 |
5 |
3 |
1 |
3 |
(4, 2, 0, 2) |
3m: 3, 4, 1 |
| 36. |
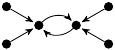 |
92 (10 kB) |
z3/16 − 7z/4 + 1
−9z3/10 + 21z/10 + 1 |
16 |
21 |
6 |
3 |
2 |
1 |
2 |
(4, 0, 0, 2) |
2m: 2, 4 |
| 37. |
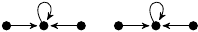 |
1 (89 B) |
−z3/16 + 7z/4 + 1 |
16 |
28 |
6 |
2 |
1 |
2 |
1, 1 |
(4, 0, 0, 2) |
1m: 2, 4 |
| 38. |
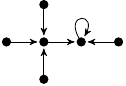 |
51 (5 kB) |
3z3/16 − 7z/12 + 1
2z3/15 − 38z/15 + 1 |
16 |
38 |
6 |
3 |
1 |
1 |
1 |
(4, 0, 0, 2) |
1m: 1, 2, 3 |
| 39. |
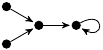 |
2 (133 B) |
3z3/16 − 9z/4 + 1 |
16 |
36 |
4 |
3 |
1 |
1 |
1 |
(2, 0, 2, 0) |
1m: 1, 1, 2 |
| 40. |
 |
1 (88 B) |
9z3/16 − 3z/4 + 1 |
16 |
16 |
5 |
2 |
1 |
3 |
1, 1, 1 |
(2, 1, 2, 0) |
1m: 3, 2 |
| 41. |
 |
1 (78 B) |
−9z3/16 + 3z/4 + 1 |
16 |
16 |
4 |
3 |
2 |
1 |
2 |
(2, 0, 2, 0) |
2m: 2, 2 |
| 42. |
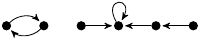 |
1 (86 B) |
−16z3/15 + 16z/15 + 1 |
16 |
16 |
6 |
3 |
2 |
2 |
1, 2 |
(2, 3, 0, 1) |
1m: 1, 2, 1
2m: 2 |
| 43. |
 |
88 (10 kB) |
9z3/10 − 21z/10 + 1 |
21 |
21 |
7 |
2 |
1 |
3 |
1, 1, 1 |
(4, 1, 0, 2) |
1m: 3, 4 |
| 44. |
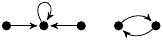 |
11 (1 kB) |
25z3/12 − 25z/12 + 1 |
25 |
25 |
5 |
2 |
2 |
2 |
1, 2 |
(2, 2, 0, 1) |
1m: 1, 2
2m: 2 |
| 45. |
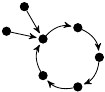 |
1 (165 B) |
z3/12 − 25z/12 + 1 |
25 |
25 |
7 |
6 |
5 |
1 |
5 |
(2, 4, 0, 1) |
5m: 5, 2 |
| 46. |
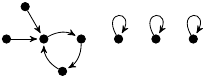 |
1 (89 B) |
−z3/12 + 25z/12 + 1 |
25 |
25 |
8 |
4 |
3 |
4 |
1, 1, 1, 3 |
(2, 5, 0, 1) |
1m: 3
3m: 3, 2 |
| 47. |
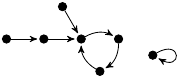 |
1 (90 B) |
3z3/4 − 25z/12 + 1 |
25 |
25 |
7 |
5 |
3 |
2 |
1, 3 |
(2, 4, 0, 1) |
1m: 1
3m: 3, 2, 1 |
| 48. |
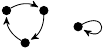 |
4 (331 B) |
7z3/6 − 25z/6 + 1 |
25 |
25 |
4 |
3 |
3 |
2 |
1, 3 |
(0, 4, 0, 0) |
1m: 1
3m: 3 |
| 49. |
 |
11 (1 kB) |
−2z3/15 + 19z/30 + 1 |
30 |
30 |
5 |
3 |
1 |
1 |
1 |
(2, 2, 0, 1) |
1m: 1, 2, 2 |
| 50. |
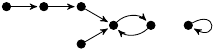 |
1 (105 B) |
−z3/3 + 37z/12 + 1 |
37 |
37 |
7 |
5 |
2 |
2 |
1, 2 |
(2, 4, 0, 1) |
1m: 1
2m: 2, 2, 1, 1 |
| 51. |
 |
1 (101 B) |
−4z3/3 + 37z/12 + 1 |
37 |
37 |
6 |
5 |
1 |
1 |
1 |
(2, 3, 0, 1) |
1m: 1, 2, 1, 1, 1 |
| 52. |
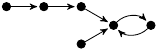 |
2 (368 B) |
−32z3/3 + 37z/6 + 1 |
37 |
64 |
6 |
5 |
2 |
1 |
2 |
(2, 3, 0, 1) |
2m: 2, 2, 1, 1 |
| 53. |
 |
2 (240 B) |
32z3/15 − 47z/15 + 1 |
47 |
47 |
5 |
2 |
2 |
4 |
1, 1, 1, 2 |
(0, 5, 0, 0) |
1m: 3
2m: 2 |
| 54. |
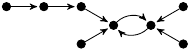 |
2 (223 B) |
z3/48 − 19z/12 + 1 |
48 |
76 |
8 |
5 |
2 |
1 |
2 |
(4, 2, 0, 2) |
2m: 2, 4, 1, 1 |
| 55. |
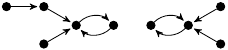 |
2 (230 B) |
z3/48 − 31z/12 + 1
−49z3/48 + 19z/12 + 1 |
48 |
76 |
9 |
4 |
2 |
2 |
2, 2 |
(4, 3, 0, 2) |
2m: 4, 4, 1 |
| 56. |
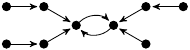 |
1 (118 B) |
25z3/24 − 49z/24 + 1 |
49 |
49 |
9 |
4 |
2 |
1 |
2 |
(4, 3, 0, 2) |
2m: 2, 4, 3 |
| 57. |
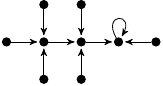 |
1 (131 B) |
5z3/12 − 49z/60 + 1 |
60 |
60 |
9 |
4 |
1 |
1 |
1 |
(6, 0, 0, 3) |
1m: 1, 2, 3, 3 |
| 58. |
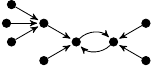 |
3 (394 B) |
−5z3/12 + 49z/60 + 1 |
60 |
60 |
9 |
4 |
2 |
1 |
2 |
(6, 0, 0, 3) |
2m: 2, 4, 3 |
| 59. |
 |
1 (77 B) |
6z3/5 − 61z/30 + 1 |
61 |
61 |
6 |
5 |
4 |
1 |
4 |
(2, 3, 0, 1) |
4m: 4, 2 |
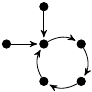
| 60. |
 |
1 (118 B) |
z3/6 − 73z/24 + 1 |
73 |
73 |
8 |
4 |
2 |
1 |
2 |
(4, 2, 0, 2) |
2m: 2, 2, 4 |
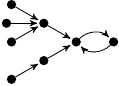
| 61. |
 |
2 (465 B) |
−z3/6 + 73z/24 + 1 |
73 |
73 |
6 |
4 |
1 |
1 |
1 |
(2, 3, 0, 1) |
1m: 1, 2, 2, 1 |
| 62. |
 |
1 (84 B) |
z3/30 − 79z/30 + 1 |
79 |
79 |
7 |
4 |
2 |
2 |
2, 2 |
(2, 4, 0, 1) |
2m: 4, 2, 1 |
| 63. |
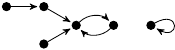 |
3 (348 B) |
49z3/30 − 79z/30 + 1 |
79 |
79 |
6 |
4 |
2 |
2 |
1, 2 |
(2, 3, 0, 1) |
1m: 1
2m: 2, 2, 1 |
| 64. |
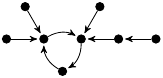 |
2 (303 B) |
−z3/30 + 91z/30 + 1 |
91 |
91 |
8 |
5 |
3 |
1 |
3 |
(4, 2, 0, 2) |
3m: 3, 4, 1 |
| 65. |
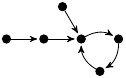 |
1 (86 B) |
8z3/15 − 121z/30 + 1 |
121 |
121 |
6 |
5 |
3 |
1 |
3 |
(2, 3, 0, 1) |
3m: 3, 2, 1 |
| 66. |
 |
4 (683 B) |
121z3/80 − 91z/20 + 1 |
121 |
364 |
9 |
2 |
1 |
3 |
1, 1, 1 |
(6, 0, 0, 3) |
1m: 3, 6 |
| 67. |
 |
1 (94 B) |
−121z3/80 + 71z/20 + 1 |
121 |
284 |
6 |
2 |
2 |
3 |
2, 2, 2 |
(0, 6, 0, 0) |
2m: 6 |
| 68. |
 |
5 (373 B) |
18z3/125 − 3z/10 + 1
144z3 − 12z + 1 |
125 |
144 |
4 |
2 |
1 |
3 |
1, 1, 1 |
(1, 2, 1, 0) |
1m: 3, 1 |
| 69. |
 |
3 (215 B) |
16z3/125 − 12z/5 + 1
−121z3/250 + 3z/10 + 1 |
125 |
250 |
4 |
2 |
2 |
2 |
1, 2 |
(1, 2, 1, 0) |
1m: 1, 1
2m: 2 |
| 70. |
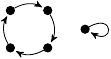 |
1 (164 B) |
3z3/128 − 55z/24 + 1 |
128 |
880 |
5 |
4 |
4 |
2 |
1, 4 |
(0, 5, 0, 0) |
1m: 1
4m: 4 |
| 71. |
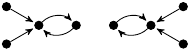 |
3 (484 B) |
−147z3/80 + 31z/60 + 1 |
147 |
441 |
8 |
3 |
2 |
2 |
2, 2 |
(4, 2, 0, 2) |
2m: 4, 4 |
| 72. |
 |
1 (95 B) |
−z3/120 + 169z/120 + 1 |
169 |
169 |
7 |
4 |
1 |
3 |
1, 1, 1 |
(2, 4, 0, 1) |
1m: 3, 2, 1, 1 |
| 73. |
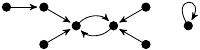 |
1 (115 B) |
49z3/120 − 169z/120 + 1 |
169 |
169 |
8 |
4 |
2 |
2 |
1, 2 |
(4, 2, 0, 2) |
1m: 1
2m: 2, 4, 1 |
| 74. |
 |
1 (130 B) |
−169z3/96 + 109z/24 + 1 |
169 |
436 |
8 |
3 |
2 |
3 |
2, 2, 2 |
(2, 5, 0, 1) |
2m: 6, 2 |
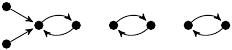
| 75. |
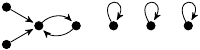 |
1 (214 B) |
−147z3/10 + 181z/30 + 1 |
181 |
441 |
7 |
3 |
2 |
4 |
1, 1, 1, 2 |
(2, 4, 0, 1) |
1m: 3
2m: 2, 2 |
| 76. |
 |
1 (120 B) |
z3/240 − 151z/60 + 1 |
240 |
604 |
10 |
3 |
2 |
3 |
2, 2, 2 |
(4, 4, 0, 2) |
2m: 6, 4 |
| 77. |
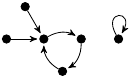 |
1 (99 B) |
243z3/10 − 151z/30 + 1 |
243 |
729 |
6 |
4 |
3 |
2 |
1, 3 |
(2, 3, 0, 1) |
1m: 1
3m: 3, 2 |
| 78. |
 |
2 (163 B) |
−49z3/250 + 27z/10 + 1
−289z3/16 + 27z/4 + 1 |
250 |
289 |
4 |
4 |
2 |
1 |
2 |
(1, 2, 1, 0) |
2m: 2, 1, 1 |
| 79. |
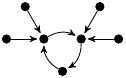 |
1 (119 B) |
27z3/256 − 133z/48 + 1 |
256 |
2128 |
7 |
4 |
3 |
1 |
3 |
(4, 1, 0, 2) |
3m: 3, 4 |
az3 + bz
Table 2. Preperiodic point portraits of polynomials of the form az3 + bz with H(a) and H(b) less than 300
| # |
Γ |
N |
f(z) |
H |
p |
c |
l |
k |
cycles |
degree |
structure |
| 1. |
 |
94,459 (5 MB) |
z3 |
1 |
3 |
1 |
1 |
3 |
1, 1, 1 |
(0, 3, 0, 0) |
1m: 3 |
| 2. |
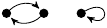 |
94,459 (4 MB) |
−z3 |
1 |
3 |
2 |
2 |
2 |
1, 2 |
(0, 3, 0, 0) |
1m: 1
2m: 2 |
| 3. |
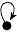 |
2,072,790,590 (32 kB) |
z3 + z |
1 |
1 |
1 |
1 |
1 |
1 |
(0, 1, 0, 0) |
1m: 1 |
| 4. |
 |
108,794 (6 MB) |
z3 − z |
1 |
3 |
2 |
1 |
1 |
1 |
(2, 0, 0, 1) |
1m: 1, 2 |
| 5. |
 |
2 (133 B) |
z3 − 3z |
3 |
5 |
2 |
1 |
3 |
1, 1, 1 |
(2, 1, 2, 0) |
1m: 3, 2 |
| 6. |
 |
2 (125 B) |
−z3 + 3z |
3 |
5 |
3 |
2 |
2 |
1, 2 |
(2, 1, 2, 0) |
1m: 1
2m: 2, 2 |
| 7. |
 |
201 (15 kB) |
3z3 − z/3 |
3 |
5 |
2 |
1 |
3 |
1, 1, 1 |
(2, 2, 0, 1) |
1m: 3, 2 |
| 8. |
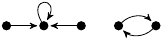 |
201 (14 kB) |
−3z3 + z/3 |
3 |
5 |
2 |
2 |
2 |
1, 2 |
(2, 2, 0, 1) |
1m: 1, 2
2m: 2 |
| 9. |
 |
174 (13 kB) |
z3 − 5z/4 |
5 |
5 |
2 |
2 |
4 |
1, 1, 1, 2 |
(0, 5, 0, 0) |
1m: 3
2m: 2 |
| 10. |
 |
116 (6 kB) |
2z3 − 5z/2 |
5 |
5 |
2 |
2 |
3 |
1, 2, 2 |
(0, 5, 0, 0) |
1m: 1
2m: 4 |
| 11. |
 |
46 (3 kB) |
3z3/2 − z/6 |
6 |
5 |
3 |
1 |
1 |
1 |
(2, 2, 0, 1) |
1m: 1, 2, 2 |
| 12. |
 |
149 (16 kB) |
2z3 − 7z/2 |
7 |
7 |
2 |
1 |
3 |
1, 1, 1 |
(4, 1, 0, 2) |
1m: 3, 4 |
| 13. |
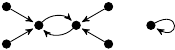 |
149 (16 kB) |
−2z3 + 7z/2 |
7 |
7 |
3 |
2 |
2 |
1, 2 |
(4, 1, 0, 2) |
1m: 1
2m: 2, 4 |
| 14. |
 |
8 (878 B) |
3z3/2 − 13z/6 |
13 |
9 |
3 |
2 |
3 |
1, 2, 2 |
(4, 3, 0, 2) |
1m: 1
2m: 4, 4 |
| 15. |
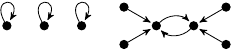 |
2 (254 B) |
3z3 − 13z/12 |
13 |
9 |
3 |
2 |
4 |
1, 1, 1, 2 |
(4, 3, 0, 2) |
1m: 3
2m: 2, 4 |
| 16. |
 |
2 (254 B) |
−3z3 + 13z/12 |
13 |
9 |
2 |
2 |
4 |
1, 1, 1, 2 |
(4, 3, 0, 2) |
1m: 3, 4
2m: 2 |
| 17. |
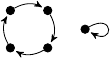 |
8 (444 B) |
6z3/5 − 17z/6 |
17 |
5 |
4 |
4 |
2 |
1, 4 |
(0, 5, 0, 0) |
1m: 1
4m: 4 |
| 18. |
 |
1 (139 B) |
3z3/2 − 19z/6 |
19 |
11 |
3 |
1 |
3 |
1, 1, 1 |
(4, 5, 0, 2) |
1m: 3, 4, 4 |
| 19. |
 |
1 (136 B) |
−3z3/2 + 19z/6 |
19 |
11 |
4 |
2 |
2 |
1, 2 |
(4, 5, 0, 2) |
1m: 1
2m: 2, 4, 4 |
| 20. |
 |
3 (280 B) |
3z3/2 − z/24 |
24 |
7 |
3 |
1 |
3 |
1, 1, 1 |
(2, 4, 0, 1) |
1m: 3, 2, 2 |
| 21. |
 |
3 (269 B) |
−3z3/2 + z/24 |
24 |
7 |
3 |
2 |
2 |
1, 2 |
(2, 4, 0, 1) |
1m: 1, 2, 2
2m: 2 |
| 22. |
 |
4 (706 B) |
3z3 − 25z/12 |
25 |
7 |
2 |
2 |
3 |
1, 2, 2 |
(2, 4, 0, 1) |
1m: 1, 2
2m: 4 |
| 23. |
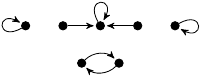 |
4 (370 B) |
3z3/2 − 25z/24 |
25 |
7 |
2 |
2 |
4 |
1, 1, 1, 2 |
(2, 4, 0, 1) |
1m: 3, 2
2m: 2 |
| 24. |
 |
5 (401 B) |
5z3/3 − 34z/15 |
34 |
7 |
2 |
2 |
5 |
1, 1, 1, 2, 2 |
(0, 7, 0, 0) |
1m: 3
2m: 4 |
| 25. |
 |
5 (382 B) |
−5z3/3 + 34z/15 |
34 |
7 |
2 |
2 |
4 |
1, 2, 2, 2 |
(0, 7, 0, 0) |
1m: 1
2m: 6 |
| 26. |
 |
2 (284 B) |
3z3 − 37z/12 |
37 |
11 |
3 |
2 |
4 |
1, 1, 1, 2 |
(4, 5, 0, 2) |
1m: 3, 4, 2
2m: 2 |
| 27. |
 |
2 (284 B) |
−3z3 + 37z/12 |
37 |
11 |
4 |
2 |
4 |
1, 1, 1, 2 |
(4, 5, 0, 2) |
1m: 3
2m: 2, 4, 2 |
| 28. |
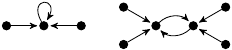 |
5 (637 B) |
3z3/2 − 49z/24 |
49 |
9 |
3 |
2 |
2 |
1, 2 |
(6, 0, 0, 3) |
1m: 1, 2
2m: 2, 4 |
| 29. |
 |
5 (658 B) |
−3z3/2 + 49z/24 |
49 |
9 |
2 |
1 |
3 |
1, 1, 1 |
(6, 0, 0, 3) |
1m: 3, 6 |
| 30. |
 |
1 (132 B) |
3z3/2 − 73z/24 |
73 |
11 |
3 |
2 |
4 |
1, 2, 2, 2 |
(4, 5, 0, 2) |
1m: 1
2m: 6, 4 |
| 31. |
 |
1 (137 B) |
−3z3/2 + 73z/24 |
73 |
11 |
3 |
2 |
5 |
1, 1, 1, 2, 2 |
(4, 5, 0, 2) |
1m: 3
2m: 4, 4 |
| 32. |
 |
2 (256 B) |
7z3/6 − 163z/42 |
163 |
9 |
4 |
2 |
2 |
1, 2 |
(4, 3, 0, 2) |
1m: 1
2m: 2, 4, 2 |
| 33. |
 |
2 (266 B) |
−7z3/6 + 163z/42 |
163 |
9 |
3 |
1 |
3 |
1, 1, 1 |
(4, 3, 0, 2) |
1m: 3, 4, 2 |
| 34. |
 |
1 (160 B) |
6z3/5 − 169z/120 |
169 |
11 |
3 |
2 |
4 |
1, 1, 1, 2 |
(6, 2, 0, 3) |
1m: 3, 2
2m: 2, 4 |
| 35. |
 |
1 (161 B) |
−6z3/5 + 169z/120 |
169 |
11 |
2 |
2 |
4 |
1, 1, 1, 2 |
(6, 2, 0, 3) |
1m: 3, 6
2m: 2 |
| 36. |
 |
1 (111 B) |
6z3/5 − 289z/120 |
289 |
9 |
2 |
2 |
4 |
1, 2, 2, 2 |
(2, 6, 0, 1) |
1m: 1, 2
2m: 6 |
| 37. |
 |
1 (116 B) |
−6z3/5 + 289z/120 |
289 |
9 |
2 |
2 |
5 |
1, 1, 1, 2, 2 |
(2, 6, 0, 1) |
1m: 3, 2
2m: 4 |
Published: 28 Mar 2021Last modified: 28 Mar 2021