© | Dror Bar-Natan: Knot Atlas: KnotTheory`:               This page is passe. Go here instead!

next up previous contents index
Next: 9 Lightly Documented Features Up: 8 Extras Previous: 8 Extras   Contents   Index

Subsections


8.1 Drawing with TubePlot

In[1]

In[2]:= ?TubePlot
TubePlot[gamma, {t, t0, t1}, r, opts] plots the space curve gamma with the variable t running from t0 to t1, as a tube of radius r. The available options are TubeSubdivision, TubeFraming and TubePlotPrelude. All other options are passed on to Graphics3D. TubePlot[TorusKnot[m, n], opts] produces a tube plot of the (m,n) torus knot.

In[3]:= Options[TubePlot]
{TubeSubdivision -> {50, 12}, TubeFraming -> Normal, TubePlotPrelude -> {}}

Thus here's a thin unknot: 

In[4]:=  
Show[TubePlot[{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.1]]
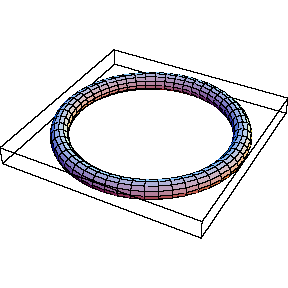Out[4]=
-Graphics-

In[5]:= ?TubeSubdivision
TubeSubdivision is an option for TubePlot. TubePlot[__, TubeSubdivision -> {l, m} draws the tube subdivided to l pieces lengthwise and m pieces around. The default is TubeSubdivision -> {50, 12}.

In[6]:= ?TubeFraming
TubeFraming is an option for TubePlot. TubePlot[gamma, {t, __}, _, TubeFraming -> n] sets the framing of the tube (visible when TubeSubdivision -> {l, m} with small m) to be the vector n, which in itself may be a function of t. Thus TubeFraming -> {0,0,1} is "blackboard framing". TubeFraming -> Normal (default) uses the normal vector of the curve gamma.

In[7]:= ?TubePlotPrelude
TubePlotPrelude is an option for TubePlot. Its value is passed to Graphics3D before the main part of the plot, allowing to set various graphics options. For example, TubePlotPrelude -> EdgeForm[{}] will suppress the drawing of edges between the polygons making up the tube. The default is TubePlotPrelude -> {}.

Here's the same unknot, made thicker and not as smooth: 

In[8]:=  
Show[TubePlot[
   {Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.3, TubeSubdivision -> {6, 3}
 ]]
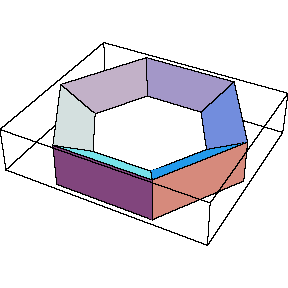Out[8]=
-Graphics-

Let's play with the framing now: 

In[9]:=  
Show[TubePlot[
   {Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.2,
   TubeSubdivision -> {50, 2},
   TubeFraming -> {Cos[2t]Cos[t], Cos[2t]Sin[t], Sin[3t]}
 ]]
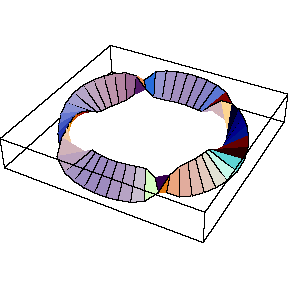Out[9]=
-Graphics-

Here's an example that uses a prelude and passes options on to Graphics3D: 

In[10]:=  
Show[TubePlot[
   {Cos[2t], Sin[2t], 0} +
     0.5{Cos[3t]Cos[2t], Cos[3t]Sin[2t], -Sin[3t]},
   {t, 0, 2Pi}, 1/3,
   TubeSubdivision -> {280, 12}, TubeFraming -> {0,0,1},
   TubePlotPrelude -> EdgeForm[{}],
   Boxed -> False, ViewPoint -> {0,0,1}
 ]]
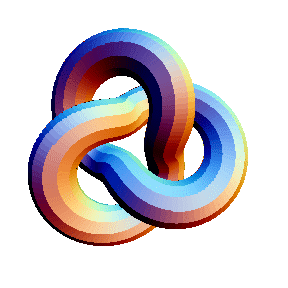Out[10]=
-Graphics-

The last example serves as the basis for the definition of TubePlot[TorusKnot[m, n]]. Here's a final example: 

In[11]:=  
Show[TubePlot[TorusKnot[3, 5]]]
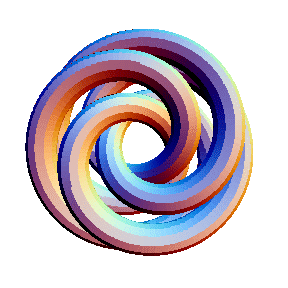Out[11]=
-Graphics-

8.1.1 Standalone TubePlot

There may be some independent interest in the routine TubePlot, and hence it is available also as an independent package. Here it is: TubePlot.m.


Dror Bar-Natan 2005-09-14