| © | Dror Bar-Natan: Classes: 2014-15: Math 475 - Problem Solving Seminar: | (32) |
Next: Blackboards for Thursday February 26
Previous: Handout for February 24, "Divide into Cases" and "Work Backwards" |
Reading. Sections 1.8 and 2.6 of Larson's textbook.
Next Quiz. Tuesday March 3 on these two sections and this handout.
Problem 1 (Larson's 2.5.11, modified).
Problem 2 (Larson's 2.5.13).

Problem 3 (Larson's 1.8.1, modified).
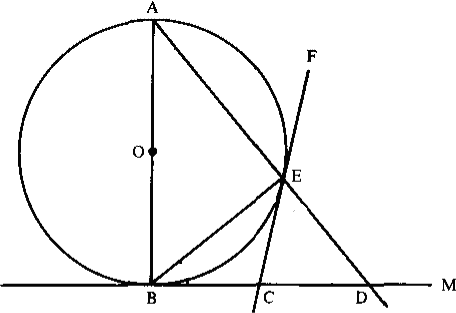
Problem 4 (Larson's 1.8.3). In the figure on the right, everything is as it seems: $O$ is the centre, $AB$ is a diameter, $CE$ and $BC$ are tangents, and all lines are straight. Show that $BC=CD$.
The Pigeonhole Principle. If 101 pigeons are put in 100 pigeonholes, at least one of the pigeonholes will be overcrowded. Or more generally,
If $kn+1$ objects are put in $n$ boxes, at least one of the boxes contains at least $k+1$ objects.
Problem 5 (Larson's 2.6.1). Given $n+1$ positive integers, none of which exceeds $2n$, show that one of these integers divides another of these integers.
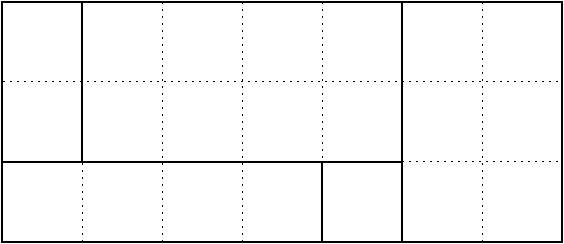
Problem 6 (Larson's 2.6.3, modified). The points on a $3\times 7$ rectangular grid are coloured $Q$ and $M$. Show that you can find a rectangle among these points, whose sides are parallel to the grid axes, and all of whose corners are coloured the same way.
Problem 7 (off topic, but fun). A rectangle is said to be "part whole" if the length of at least one of its sides is a whole number. Prove that if a rectangle $R$ can be partitioned into part whole subrectangles, then $R$ is part whole.
Hint. Consider $\int e^{2\pi i(x+y)}dx\,dy$. (!?!!)
New! I just learned of an article that has 14 proofs of this result! Fourteen Proofs of a Result About Tiling a Rectangle by Stan Wagon, The American Mathematical Monthly 94-7 (1987) 601-617.
Problem 8 (Larson's 2.6.6). If 20 integers are chosen from within the elements of the arithmetic progression 1,4,7,...,100, show that you can find two of them whose sum is 104.
Problem 9 (Larson's 2.6.10, expanded).
Problem 10 (Larson's 2.6.11, abbreviated).