Term Exam 3
University of Toronto, February 7, 2005
Solve all of the following 4 problems.
Each problem is worth 25 points.
Write your answers in the space below the problems and on the front
sides of the extra pages; use the back of the pages for scratch paper.
Only work appearing on the front side of pages will be graded. Write
your name and student number on each page. If you need more paper
please ask the tutors. You have an hour and 50 minutes.
Allowed Material: Any calculating device that is not
capable of displaying text.
Good Luck!
Problem 1.
- Compute
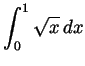 .
.
- Compute
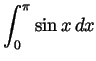 .
.
- For
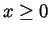 , compute
, compute
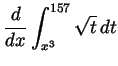 .
.
Problem 2.
- Perhaps using L'Hôpital's law, compute
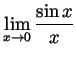 and
and
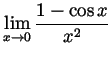 .
.
- Use these results to give educated guesses for the values of
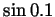 and
and 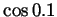 (no calculators, please).
(no calculators, please).
Problem 3.
- State the ``one partition for every
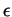 '' criterion of the
integrability of a bounded function
'' criterion of the
integrability of a bounded function 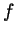 defined on an interval
defined on an interval
![$ [a,b]$](img13.gif) .
.
- Let
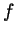 be an increasing function on
be an increasing function on ![$ [0,1]$](img14.gif) and let
and let 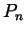 be the
partition defined by
be the
partition defined by 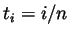 , for
, for
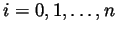 . Write simple formulas
for
. Write simple formulas
for 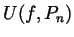 and for
and for 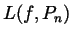 .
.
- Under the same conditions, write a very simple formula for
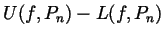 .
.
- Prove that an increasing function on
![$ [0,1]$](img14.gif) is integrable.
is integrable.
Problem 4.
- Show that the function
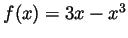 is monotone on the interval
is monotone on the interval
![$ [-1,1]$](img22.gif) .
.
- Deduce that for every
![$ c\in[-2,2]$](img23.gif) the equation
the equation 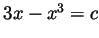 has a
unique solution
has a
unique solution 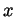 in the range
in the range
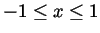 .
.
- For
![$ c\in[-2,2]$](img23.gif) , let
, let 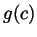 be the unique
be the unique 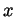 in the range
in the range
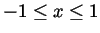 for which
for which 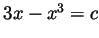 . Write a formula for
. Write a formula for 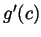 and
simplify it as much as you can. Your end result may still contain
and
simplify it as much as you can. Your end result may still contain 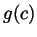 in
it, but not
in
it, but not 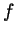 ,
, 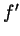 or
or 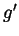 .
.
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2005-02-04
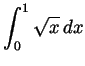 .
.
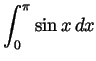 .
.
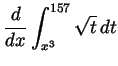 .
.
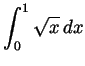 .
.
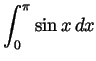 .
.
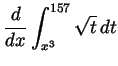 .
.
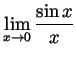 and
and
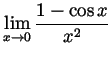 .
.