| © | Dror Bar-Natan: Classes: 2004-05: Math 157 - Analysis I: | (27) |
Next: Solution of Term Exam 1
Previous: Class Notes for Thursday October 14, 2004 |
Solve 4 of the following 5 problems. Each problem is worth 25 points. If you solve more than 4 problems indicate very clearly which ones you want graded; otherwise a random one will left out at grading and it may be your best one! Write your answers in the space below the problems and on the front sides of the extra pages; use the back of the pages for scratch paper. Only work appearing on the front side of pages will be graded. Write your name and student number on each page. If you need more paper please ask the tutors. You have an hour and 50 minutes.
Allowed Material: Any calculating device that is not capable of displaying text.
Problem 1. Find formulas for
![]() ,
,
![]() and
and
![]() in terms of
in terms of
![]() . (You may use any
formula proven in class; you need to quote such formulae, though you
don't need to reprove them).
. (You may use any
formula proven in class; you need to quote such formulae, though you
don't need to reprove them).
Problem 2.
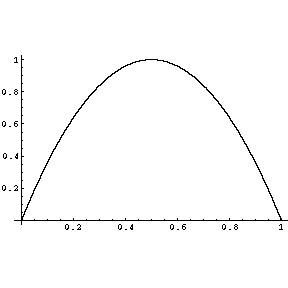
Problem 3. A function ![]() is defined for
is defined for
![]() and has the graph plotted above.
and has the graph plotted above.
Problem 4.
Problem 5. Give examples to show that the
following definitions of
![]() do not
agree with the standard one:
do not
agree with the standard one: