Homework Assignment 3
Assigned Tuesday September 23; due Friday October 3, 2PM,
at
SS 1071
Required email. The class photo will be on
the class' web site in a day or two and you are all required to find
it, find yourself in the photo, and send me an email message (either
using the feedback form on the class' web site or using my regular
email address) with the following information:
- Where are you in the picture? (Use the supplied grid. If your
square has more than one face in it, add something like ``I'm the guy
with the red hair''.)
- Your name.
- Your email address.
- Your telephone number (optional).
- Which of the last four pieces of information do you allow me to
put on the web? If you don't write anything about this, I'll assume
that your location in the photo, your name and your email address are
public but that your phone number is to be kept confidential.
Your email is due like the rest of this assignment, on Friday October 3
at 2PM. If you aren't in the picture at all, talk to me after class and
I'll take a (small) picture of you on the spot and edit it into the main
picture.
Required reading. All of Spivak Chapters 2 and 3.
To be handed in.
From Spivak Chapter 2: 1, 5.
From Spivak Chapter 3: 6, 13.
Recommended for extra practice.
From Spivak Chapter 2: 3, 4, 12, 22.
From Spivak Chapter 3: 1, 7, 21.
An extra problem: (recommended, but do not
submit) Is there a problem with the following inductive proof that all
horses are of the same color?
We assert that in all sets with precisely 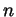 horses, all horses are of the
same color. For
horses, all horses are of the
same color. For 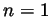 , this is obvious: it is clear that in a set with just
one horse, all horses are of the same color. Now assume our assertion is
true for all sets with
, this is obvious: it is clear that in a set with just
one horse, all horses are of the same color. Now assume our assertion is
true for all sets with 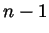 horses, and let us be given a set with
horses, and let us be given a set with 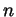 horses in it. By the inductive assumption, the first
horses in it. By the inductive assumption, the first 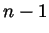 of those are of
the same color and also the last
of those are of
the same color and also the last 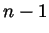 of those. Hence they are all of the
same color as illustrated below:
of those. Hence they are all of the
same color as illustrated below:
(The horses surrounded by round brackets  are all of the same
color. The horses surrounded by square brackets
are all of the same
color. The horses surrounded by square brackets ![$ [\cdots]$](img6.gif) are all of
the same color. Therefore the first and the last horses have the same
color as the ones in the middle group, and hence all horses are of the
same color.)
are all of
the same color. Therefore the first and the last horses have the same
color as the ones in the middle group, and hence all horses are of the
same color.)
Just for fun.
From Spivak Chapter 2: 27, 28.
A little more on Chapter 2, Problem 22:
- We know that if
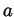 and
and 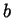 are non-negative then
are non-negative then
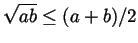 . This is the same as saying that
. This is the same as saying that
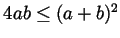 ,
which is the same as saying that the area of four
,
which is the same as saying that the area of four 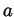 by
by 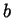 rectangles is
less than or equal to the area of a square with side
rectangles is
less than or equal to the area of a square with side 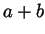 . Can you
actually fit four
. Can you
actually fit four 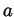 by
by 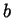 rectangles inside a square of side
rectangles inside a square of side 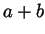 without overlaps? It's fun and not too hard.
without overlaps? It's fun and not too hard.
- We know that if
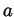 ,
, 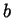 and
and 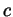 are non-negative then
are non-negative then
![$ \sqrt[3]{abc}\leq(a+b+c)/3$](img13.gif) . This is the same as saying that
. This is the same as saying that
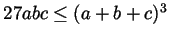 , which is the same as saying that the volume of 27
, which is the same as saying that the volume of 27
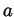 by
by 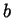 by
by 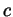 rectangular boxes is less than or equal to the volume
of a cube with side
rectangular boxes is less than or equal to the volume
of a cube with side 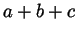 . Can you actually fit 27 such
. Can you actually fit 27 such 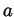 by
by 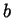 by
by 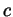 rectangular boxes inside a cube of side
rectangular boxes inside a cube of side 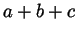 without overlaps? This is
also fun, but quite hard. You have no chance of doing it without a physical
model. Make yourself one!
without overlaps? This is
also fun, but quite hard. You have no chance of doing it without a physical
model. Make yourself one!
- The corresponding problem in 4D, involving 256 boxes of size
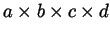 , is actually a little easier, though trickier, than the
3D problem. Can you do it?
, is actually a little easier, though trickier, than the
3D problem. Can you do it?
- The corresponding problem in 5D, involving 3,125 boxes of size
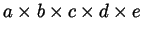 , is an open problem -- meaning that
nobody knows how to solve it. Can you?
, is an open problem -- meaning that
nobody knows how to solve it. Can you?
The generation of this document was assisted by
LATEX2HTML.
Dror Bar-Natan
2003-10-21
![]() horses, all horses are of the
same color. For
horses, all horses are of the
same color. For ![]() , this is obvious: it is clear that in a set with just
one horse, all horses are of the same color. Now assume our assertion is
true for all sets with
, this is obvious: it is clear that in a set with just
one horse, all horses are of the same color. Now assume our assertion is
true for all sets with ![]() horses, and let us be given a set with
horses, and let us be given a set with ![]() horses in it. By the inductive assumption, the first
horses in it. By the inductive assumption, the first ![]() of those are of
the same color and also the last
of those are of
the same color and also the last ![]() of those. Hence they are all of the
same color as illustrated below:
of those. Hence they are all of the
same color as illustrated below:
![$\displaystyle \left(\begin{array}{c}
\includegraphics[width=0.6in]{RockingHorse...
...n{array}{c}
\includegraphics[width=0.6in]{RockingHorse.eps}
\end{array}\right] $](img4.gif)