Dror Bar-Natan: Classes: 2002-03: Math 157 - Analysis I: (263) Next: Homework Assignment 24
Previous: Term Exam 4

Solution of Term Exam 4

this document in PDF: Solution.pdf

Problem 1. Is there a non-zero polynomial defined on the interval $[0,\pi]$ and with values in the interval $[0,\frac12)$ so that it and all of its derivatives are integers at both the point 0 and the point $\pi$ ? In either case, prove your answer in detail. (Hint: How did we prove the irrationality of $\pi$ ?)

Solution. There isn't. Had there been one, we could reach a contradiction as in the proof of the irrationality of $\pi$ . Indeed we would have that $0<\int_0^\pi p(x)\sin x dx<\frac12\int_0^\pi \sin x dx=1$ , hence the integral $I=\int_0^\pi p(x)\sin x dx$ is not an integer. But repeated integration by parts gives

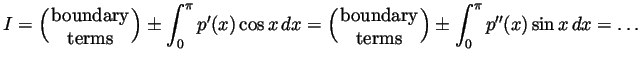
$\displaystyle I =\left(\parbox{18mm}{\centering boundary terms}\right) \pm\int_... ...{18mm}{\centering boundary terms}\right) \pm\int_0^\pi p''(x)\sin x dx =\dots$

$\displaystyle =\left(\parbox{18mm}{\centering boundary terms}\right) \pm\int_0^\pi p^{(2n)}(x)\sin x dx.$

The assumptions on $p^{(k)}(0)\in{\mathbb{Z}}$ and $p^{(k)}(\pi)\in{\mathbb{Z}}$ along with the fact that $\sin 0$ , $\sin\pi$ , $\cos 0$ and $\cos\pi$ are all integers imply that the boundary terms are all integers. If

is large enough, $p^{(2n)}=0$ and hence the remaining integral is 0. So

is an integer, and that's a contradiction.

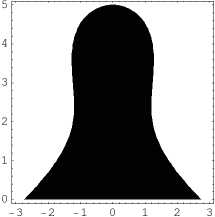Problem 2. Compute the volume of the ``Black Pawn'' on the right -- the volume of the solid obtained by revolving the solutions of the inequalities $4x^2\leq y+3-(y-3)^3$ and $y\geq 0$ about the axis (its vertical axis of symmetry). (Check that and hence the height of the pawn is ).

Solution. This is the area of the rotation solid with radius $r(y)=\frac12\sqrt{y+3-(y-3)^3}$ bounded by and . Thus

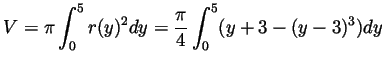
$\displaystyle V=\pi\int_0^5 r(y)^2dy = \frac{\pi}{4}\int_0^5(y+3-(y-3)^3)dy$

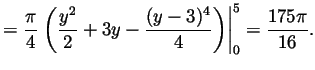
$\displaystyle =\frac{\pi}{4}\left.\left( \frac{y^2}{2}+3y-\frac{(y-3)^4}{4} \right)\right\vert _0^5 = \frac{175\pi}{16}.$

Problem 3.

Compute the degree Taylor polynomial of the function $f(x)=\frac{1}{1-x}$ around the point 0.
Write a formula for the remainder in terms of the derivative $f^{(n+1)}$ evaluated at some point $t\in[0,x]$ .
Show that at least for very small values of , $f(x)=\lim_{n\to\infty}P_n(x)$ .

Solution.

$f'=\frac{1}{(1-x)^2}$ , $f''=\frac{2}{(1-x)^3}$ , $f'''=\frac{2\cdot 3}{(1-x)^4}$ and so it can be shown by induction that $f^{(k)}=\frac{k!}{(1-x)^{k+1}}$ . Thus $f^{(k)}(0)=k!$ and hence $P_n(x)=\sum_{k=0}^n\frac{f^{(k)}(0)}{k!}x^k=\sum_{k=0}^nx^k=1+x+x^2+\dots+x^n$ .
Cauchy's formula for the remainder is $R_n(x)=f(x)-P_n(x)=\frac{f^{(n+1)}(t)}{(n+1)!}x^{n+1}= \frac{x^{n+1}}{(1-t)^{n+2}}=\frac{1}{1-t}\left(\frac{x}{1-t}\right)^{n+1}$ for some $t\in[0,x]$ .
If $\vert x\vert<\frac12$ then $\vert t\vert<\frac12$ and $\vert 1-t\vert>\frac12$ and hence $\left\vert\frac{x}{1-t}\right\vert<2\vert x\vert<1$ and thus $\vert R_n(x)\vert<\frac{1}{1-t}(2\vert x\vert)^{n+1}\to 0$ . Therefore $f(x)-P_n(x)\to 0$ , as required.

Problem 4.

Prove that if $\lim_{n\to\infty} a_n=l$ and the function is continuous at , then $\lim_{n\to\infty}f(a_n)=f(l)$
Let be a number, and define a sequence via the relations and $a_{n+1}=\frac12(a_n+b/a_n)$ for $n\geq 1$ . Assuming that this sequence is convergent to a positive limit, determine what this limit is.

Solution.

See the ``easy'' part of Theorem 1 of Spivak's Chapter 22.
Assume $\lim a_n=l>0$ . Then $l=\lim a_{n+1}=\lim\frac12(a_n+b/a_n)$ . Using the first part of this question on the function $x\mapsto\frac12(x+b/x)$ , which is continuous at , we find that $\lim\frac12(a_n+b/a_n)=\frac12(l+b/l)$ . Hence satisfies $l=\frac12(l+b/l)$ . Dividing by we get $1=\frac12+\frac{b}{2l^2}$ which is $1=\frac{b}{l^2}$ which along with implies that $l=\sqrt{b}$ .

Problem 5. Do the following series converge? Explain briefly why or why not:

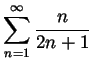$\displaystyle \sum_{n=1}^\infty \frac{n}{2n+1}$ .
Solution. $\lim_{n\to\infty}\frac{n}{2n+1}=\frac12$ hence by the vanishing test the series cannot converge.
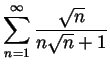$\displaystyle \sum_{n=1}^\infty \frac{\sqrt{n}}{n\sqrt{n}+1}$ .
Solution. $\frac{\sqrt{n}}{n\sqrt{n}+1}>\frac{\sqrt{n}}{2n\sqrt{n}}=\frac{1}{2n}$ . The latter is a multiple of the harmonic series which doesn't converge, hence the original series doesn't converge either.
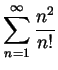$\displaystyle \sum_{n=1}^\infty \frac{n^2}{n!}$ .
Solution. Ignoring the first two terms of the series, which don't change convergence anyway,

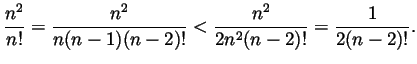
$\displaystyle \frac{n^2}{n!}=\frac{n^2}{n(n-1)(n-2)!}<\frac{n^2}{2n^2(n-2)!} =\frac{1}{2(n-2)!}.$
The latter sequence is summable as we have shown in class, hence the original series is convergent.
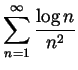$\displaystyle \sum_{n=1}^\infty \frac{\log n}{n^2}$ .
Solution. The function $f(x)=\sqrt{x}-\log x$ is positive at and simple differentiation shows that for $x\geq 1$ , hence it is increasing, and hence it is positive for all $x\geq 1$ . Thus $\frac{\log n}{n^2}<\frac{\sqrt{n}}{n^2}=\frac{1}{n^{3/2}}$ which is summable as was shown in class.
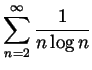$\displaystyle \sum_{n=2}^\infty \frac{1}{n\log n}$ .
Solution. That's a tough one. Here's a solution inspired by the solution to Problem 20 of Spivak's Chapter 23, which by itself is inspired by the proof of the divergence of the harmonic series:

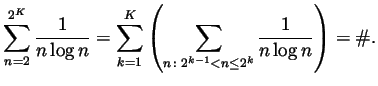
$\displaystyle \sum_{n=2}^{2^K}\frac{1}{n\log n} =\sum_{k=1}^K\left( \sum_{n\colon 2^{k-1}<n\leq 2^k}\frac{1}{n\log n} \right) = \char93 .$
If we replace each of the inner sums here by the number of terms in it times the smallest of those, which is the last of those, it only becomes smaller. Hence

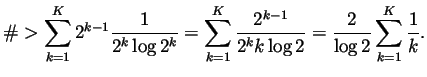
$\displaystyle \char93 >\sum_{k=1}^K 2^{k-1}\frac{1}{2^k\log 2^k} =\sum_{k=1}^K \frac{2^{k-1}}{2^kk\log2} =\frac{2}{\log2}\sum_{k=1}^K\frac1k.$
The latter are partial sums of a divergent positive series, hence they approach infinity. Therefore the partial sums $\sum_{n=2}^{2^K}\frac{1}{n\log n}$ approach infinity and our series is divergent.