Dror Bar-Natan: Classes: 2002-03: Math 157 - Analysis I:

(113)

Next: Homework Assignment 11 Previous: Class Notes for the Week of November 11 (9 of 9)

A Little on Convexity

this document in PDF: Convexity.pdf

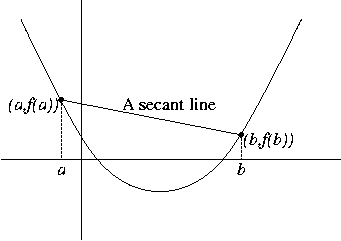
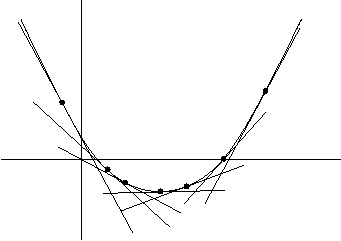
We are skipping the appendix on convexity of Spivak's Chapter 11, but it is still worthwhile to take something from it (without proof):

Theorem. The following are equivalent, for a function $f$ defined on some interval $I$ (assuming $f$ is such that these statements make sense):

1. All the secants of $f$ are above the graph of $f$.
2. For every $a,b\in I$ and every $t\in(0,1)$,
   $$f(ta+(1-t)b)<tf(a)+(1-t)f(b).$$

3. The tangents to the graph of $f$ all lie below that graph and touch it just at the points of tangency.
4. The derivative $f'$ is increasing.
5. The second derivative $f''$ is positive on $I$: $\forall x\in I f''(x)>0$. (Gary Baumgartner makes the following correction: This last statement implies all others, but it isn't implied by the others as can be seen by looking for example at $f(x)=x^4$. If all sharp inequalities in this handout are replaced by non-sharp ones (i.e., replace $>$ by $\geq$ and $<$ by $\leq$ everywhere, with similar corrections for verbal statements), then this statement becomes equivalent to all others).

If any of these statements holds, we say that ``$f$ is convex''. There is a similar theorem with all inequalities reversed, and then the name is ``$f$ is concave''.

The generation of this document was assisted by L^ATEX2HTML.