September 5, 2003
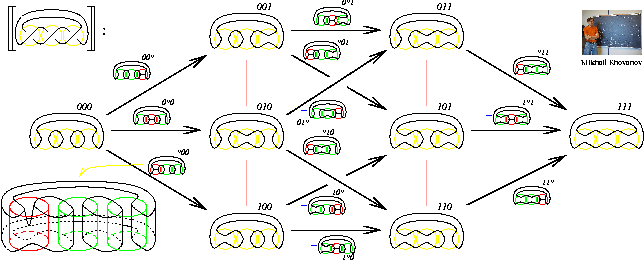
Abstract: The Jones polynomial created an industry when it was discovered in the early eighties. Yet only about four years ago Khovanov (arXiv:math.QA/9908171) found that it has a simple yet very intriguing generalization - that it is the Euler characteristic of a complex whose entire homology is invariant. And less than two years ago it was realized by Jacobsson (arXiv:math.GT/0206303) and Khovanov (arXiv:math.QA/0207264) that the resulting homology theory is functorial in the appropriate sense and leads to an invariant of 2-knots in 4-space. (And it's good to keep in mind that functoriality is the key to algebraic topology - without it algebraic topology can do little more than classify surfaces by their genus).
In my talk I will display one complicated picture and discuss it at length. Applying a certain 2D TQFT, we will get a homology theory whose Euler characteristic is the Jones polynomial. Not applying it, very cheaply we will get an invariant of tangles which is functorial under cobordisms and an invariant of 2-knots.
The Handout: NewHandout-1.pdf.
The Picture:
