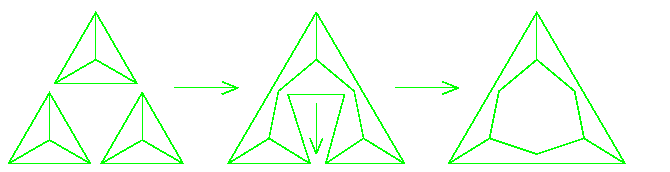

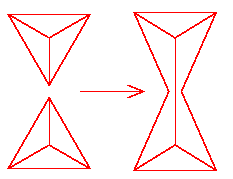
Abstract: I will present some recent speculations1 regarding the marginals of the Chern-Simons path integral measure, as observed on holonomies along embedded trivalent graphs. We will find that there is a simple and appealing axiomatic description for thereby inspired "consistent systems of marginals", which involves the Mobius band, the tetrahedron, hour glasses, and ring around the rosie dances. While the possible existence of such systems of marginals is at best shaky, we will explain that they do exist in a perturbative sense (where they provide a clean and elegant framework for Drinfel'd's theory of associators), and in a representation theoretic sense (where they relate to the theory of quantum 6j-symbols). At the very end, I will explain how we2 got there and why we care.
This abstract is at http://www.math.toronto.edu/~drorbn/Talks/UCSD-000113/.
1 The term "speculations" will be defined at the start of the talk.
2 Dylan Thurston and myself, though the former should not be held liable for the nonsense.