© | << < ? > >> |
Dror Bar-Natan:
Talks:
Khovanov Homology for Tangles and Cobordisms
Topology Seminar, University of Rochester, April 4, 2004
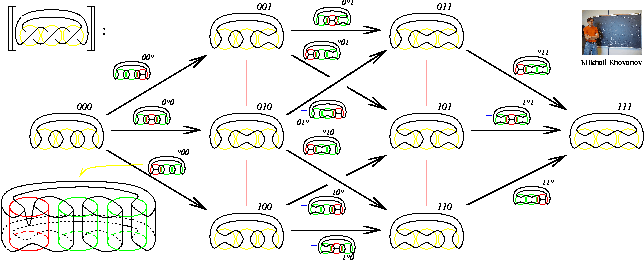
Abstract. In my talk I will display one complicated picture and
discuss it at length. Applying a certain 2D TQFT, we will get a homology
theory whose Euler characteristic is the Jones polynomial. Not applying it,
very cheaply we will get an invariant of tangles which is functorial under
cobordisms and an invariant of 2-knots.
Why is it interesting?
- It is a knot/link/tangle invariant stronger than the Jones polynomial.
- It may be stronger than the original "Khovanov Homology".
- It has several generalizations, but as a whole, we hardly understand
it. It may have significant algebraic and/or physical ramifications.
- It is functorial in the appropriate sense, and Rasmussen (math.GT/0402131
uses it to do some real topology.
Handout side 1:
NewHandout-1.pdf.
Handout side 2:
handout2.pdf.
The Picture: