International Mathematical Talent Search
International Mathematical Talent Search
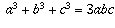 .
.
Problem 2/16. For a positive integer n, let P(n) be the product of the nonzero base 10 digits of n. Call n "prodigitious" if P(n) divides n. Show that one cannot have a sequence of fourteen consecutive positive integers that are all prodigitious.
Problem 3/16. Disks numbered 1 through n are placed in a row of squares, with one square left empty. A move consists of picking up one of the disks and moving it into the empty square, with the aim to rearrange the disks in the smallest number of moves so that disk 1 is in square 1, disk 2 is in square 2, and so on until disk n is in square n and the last square is left empty. For example, if the original arrangement is
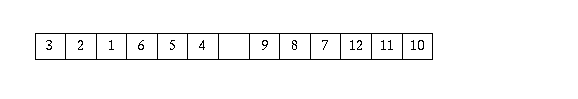
then it takes at least 14 moves; e.g., we could move the disks into the empty square in the following order: 7, 10, 3, 1, 3, 6, 4, 6, 9, 8, 9, 12, 11, 12.
What initial arrangement requires the largest number of moves if n = 1995? Specify the number of moves required.
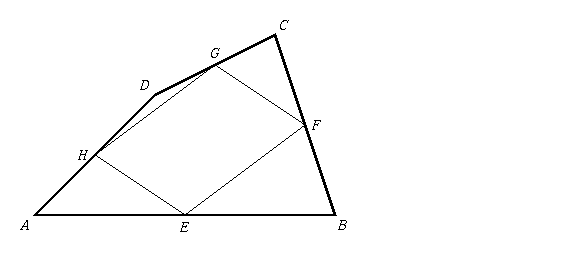
Problem 4/16. Let ABCD be an arbitrary convex quadrilateral, with E, F, G, H the midpoints of its sides, as shown in the figure below. Prove that one can piece together triangles AEH, BEF, CFG, DGH to form a parallelogram congruent to parallelogram EFGH.
Problem 5/16. An equiangular polygon ABCDEFGH has sides of length
2, 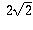 , 4,
, 4, 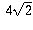 , 6, 7, 7, 8. Given that
AB = 8, find the length of EF.
, 6, 7, 7, 8. Given that
AB = 8, find the length of EF.
Solve as many of the problems as you can (you need not solve them all), and mail your solutions to:
Professor E. J. BarbeauMake sure that the front page of your solutions contains your full name and mailing address.
Department of Mathematics
University of Toronto
Toronto, ON M5S 3G3
![]() Go up to Talent Search Index
Go up to Talent Search Index![]() Go forward to Round 17
Go forward to Round 17![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page