(These buttons explained below)
Question Corner and Discussion Area
What if someone did this :This particular sum does not add up to any (finite) number. (We say that the sum diverges; you can also think of it as "adding up to infinity").and it comes to some amount. Would that number be "special"? Are there any other special constants that haven't been discovered?
To see this first note that
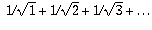is
greater than 1/1 + 1/2 + 1/3 + . . . .
The second sum is often called the harmonic series and is known to
diverge. This is because
we can regroup the terms and write it
as (1/1) + (1/2) + (1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) + . . . .
Now this sum is greater than
(1/1) + (1/2) + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) + . . . .
Note that each parenthesized group except the first adds up to 1/2. So,
after the first group, the sum is at 1. After the next two groups, the sum
as at 1 + (1/2) + (1/2) = 2. After the next two groups, the sum is
at 2 + (1/2) + (1/2) = 3. And so on. Continuing in this way, we see that
the sum eventually passes every finite number, so the total sum is
infinite.
In general there are many numbers which are defined by infinite sums. For instance e = 1 + 1/2! + 1/3! + 1/4! + . . . where n! = (n)(n-1)(n-2)· · ·(2)(1). Pi can also be expressed as a sum, although it is a bit more complicated.
Your example can be modified to add up to a finite number. For each power
p > 1, the sum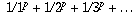 
does add up to a finite
value. But no special name is given to that value.
There are infinitely many real numbers (in fact, what mathematicians call "uncountably infinitely many" which is even more than just "infinitely many"!), so there are plenty of numbers that nobody has had occasion to think about in a special way. That doesn't mean they haven't been "discovered", though; after all, until now nobody has probably ever before written down the number
2374348627846827468726482678346278348236but that doesn't mean I somehow "discovered" it by writing it down for the first time. A "discovery" would be discovering that some number had special, unique, and important properties that no other number has.
It is difficult to say which numbers are "special."
Numbers such as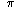 
and e are special because they occur naturally
in many situations in applied mathematics.
There are a variety of other constants in mathematics which are
somewhat less useful but nevertheless still relevant to some people.
Go backward to Finding the Ratio from the Sum of a Geometric Series Go up to Question Corner Index Go forward to A Sequence Describing a Bouncing Ball Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page