Question Corner and Discussion Area
Question Corner and Discussion Area
I heard somewhere that there is a proof that root 2 is irrational by geometric means. Does anyone know this?The geometric proof is a somewhat more awkward version of the proof that is most commonly given for the irrationality of
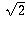 .
Its significance is mostly historical--it was the first known proof,
discovered by the Pythagoreans.
This proof was taken from Euclid's Elements, volume III.
.
Its significance is mostly historical--it was the first known proof,
discovered by the Pythagoreans.
This proof was taken from Euclid's Elements, volume III.
Let ABCD be a square (with diagonal AC) and consider the ratio AC : AB.
Suppose for contradiction that AC : AB = n : m for two positive integers
m and n which have no common divisor.
It can be seen (either by the Pythagorean Theorem or by comparing
areas) that 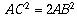 and thus
and thus 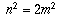 .
Note here that
.
Note here that 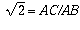 .
It follows from our assumptions that n is even and m is odd.
Since n is even, let n = 2k.
Then
.
It follows from our assumptions that n is even and m is odd.
Since n is even, let n = 2k.
Then 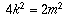 and
and 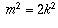 .
But this implies that m is also even, a contradiction.
Thus
.
But this implies that m is also even, a contradiction.
Thus 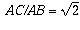 is not a rational number.
is not a rational number.
Asked by Robert Second, student, Greendale on October 3, 1997:
I don't understand how either proof of root 2 is an irrational number (the geometric method and the contradiction method) works. How does proving that numbers are even prove that root 2 is irrational??Any rational number can be expressed as a fraction in lowest terms, that is, in the form a/b where a and b have no common factors. In particular, this means that any rational number can be expressed in the form a/b where a and b aren't both even.Thanks.
To put it another way: suppose you start with some fraction a/b. It's certainly possible that a and b might both be even, but if they are, you could divide both of them by two and the fraction will still represent the same rational number. You can keep on doing this as long as they are both even. Since no integer can be divided by 2 infinitely often and remain an integer, this process must stop sometime, and you will end up with a fraction where the numerator and denominator are not both even.
For example, if you start with the fraction 8/12, after twice dividing top and bottom by 2 you end up with 2/3 and 3 is odd.
Therefore, if the square root of 2 were rational, you would be able to write it in the form a/b where a and b are not both even. However, the proof shows that this is not possible, and therefore the square root of 2 is not rational.
Asked by Bryan Low, teacher, San Leandro High School on January 3, 1998:
Why is the square root of of 2 irrational? Is there another proof besides the geometric one founded by the Pythagoreans? I have read that one on your site. I don't believe my student remeber much geometry to understand that irrational proof posted on your site.You don't need any geometry for the proof; it was just originally phrased that way because the Pythagoreans were thinking about geometry at the time.Any help will be appreciated!!!
Bryan Low
The essence of the proof is this. If the square root of two were a rational number, you could write it as a fraction a/b in lowest terms, where a and b were integers, not both even. (If a and b were both even, the fraction wouldn't be in lowest terms; you could divide top and bottom by 2, and keep doing this until one of them stops being even).
That means that, if the square root of two were a rational number, it would
be possible to find two integers a and b, not both even, such that
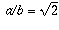 . But this is impossible, because the equation can be
written as
. But this is impossible, because the equation can be
written as
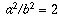 , so
, so 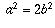 , so
a is even. That means you can write a=2k where k is an integer.
Now the equation
, so
a is even. That means you can write a=2k where k is an integer.
Now the equation 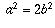 becomes
becomes 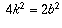 , so
, so
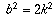 , so b would have to be even as well.
, so b would have to be even as well.
Therefore, because it is impossible to find two integers a and b with
the property that a and b are not both even and 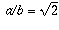 ,
the square root of two cannot be a rational number.
,
the square root of two cannot be a rational number.
![]() Go backward to How To Find The Least Common Multiple
Go backward to How To Find The Least Common Multiple![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to Which U.S. President Re-Proved the Pythagorean Theorem?
Go forward to Which U.S. President Re-Proved the Pythagorean Theorem?![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page