Question Corner and Discussion Area
Question Corner and Discussion Area
Sorry for my English.When b is a positive integer,I do not understand why we agree with the axiom :
.
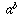 is defined to be the product
of a multiplied by itself b times.
is defined to be the product
of a multiplied by itself b times.
The question is, what is the most natural way to extend this definition
to the case when b=0? Here are several ways to see that the
definition 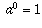 is the only reasonable one:
is the only reasonable one:
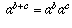 . If we want this law to still be satisfied when we extend
to the case b=0, we need to have
. If we want this law to still be satisfied when we extend
to the case b=0, we need to have
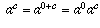 , and therefore we need to have
, and therefore we need to have
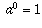 .
.
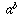 is b copies of the number a, all multiplied
together, then
is b copies of the number a, all multiplied
together, then 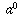 should be the "empty product" with no
factors multiplied together. In mathematics, the empty product is
defined to be 1, because multiplying by nothing at all is the same
as multiplying by 1.
should be the "empty product" with no
factors multiplied together. In mathematics, the empty product is
defined to be 1, because multiplying by nothing at all is the same
as multiplying by 1.
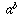 can be thought of as "start with the number 1,
then multiply by a, b times." For instance,
can be thought of as "start with the number 1,
then multiply by a, b times." For instance, 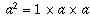 and
and 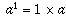 . Therefore,
. Therefore, 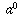 should be just 1, not multiplied
by anything else at all.
should be just 1, not multiplied
by anything else at all.
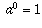 is that
is that 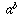 is the number of ways of
writing (in order) b numbers, each from 1 to a.
For instance,
is the number of ways of
writing (in order) b numbers, each from 1 to a.
For instance, 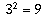 because there are nine different pairs of numbers
each of which is in the range from 1 to 3 (they are (1,1), (1,2), (1,3),
(2,1), (2,2), (2,3), (3,1), (3,2), and (3,3)).
because there are nine different pairs of numbers
each of which is in the range from 1 to 3 (they are (1,1), (1,2), (1,3),
(2,1), (2,2), (2,3), (3,1), (3,2), and (3,3)).
Therefore, 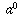 should be the number of ways of writing no numbers,
each of which is from 1 to a. There is exactly one way of doing this,
namely, don't write any numbers at all!
should be the number of ways of writing no numbers,
each of which is from 1 to a. There is exactly one way of doing this,
namely, don't write any numbers at all!
(This reason is more compelling if you make it more mathematically precise,
using the fact that 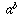 is the number of functions from a
b-element set B to an a-element set A, and when b=0 the set B
is the empty set, and there is exactly one function from the empty set into
A, namely, the empty function).
is the number of functions from a
b-element set B to an a-element set A, and when b=0 the set B
is the empty set, and there is exactly one function from the empty set into
A, namely, the empty function).
The above reasons all illustrate why defining 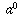 to be 1 is the
only reasonable definition.
to be 1 is the
only reasonable definition.
There's one other point worth mentioning: some of the reasons above
are less compelling when a=0. For instance, in the first reason, we
need to have 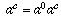 , and if a is non-zero we can divide by
, and if a is non-zero we can divide by
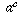 to deduce that
to deduce that 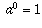 . However, if a=0 we no longer get
a reason for
. However, if a=0 we no longer get
a reason for 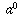 to be 1.
to be 1.
Some of the reasons are still compelling, and, especially if we are in
a context where only integer exponents are being considered, we still
normally define 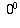 to be 1.
to be 1.
However, if we define a two-variable function 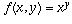 ,
then this function does not have a well-defined limit as
(x,y) -> (0,0). We can define
,
then this function does not have a well-defined limit as
(x,y) -> (0,0). We can define 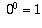 if we like,
but the limit still won't exist. In other words,
if A and B each approach zero, there's no guarantee as to
what (if anything)
if we like,
but the limit still won't exist. In other words,
if A and B each approach zero, there's no guarantee as to
what (if anything) 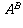 approaches. It need not approach
our definition of
approaches. It need not approach
our definition of 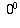 .
.
That's why, in calculus,
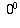 is often called an indeterminate form. If one is working
in situations where the exponent can continuously vary, it is usually
better to leave
is often called an indeterminate form. If one is working
in situations where the exponent can continuously vary, it is usually
better to leave 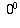 undefined to avoid making mistakes. However,
if one is working in situations in which the exponent is always
integral,
undefined to avoid making mistakes. However,
if one is working in situations in which the exponent is always
integral, 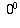 is usually defined to be 1.
is usually defined to be 1.
These complications are only for 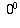 . When a is nonzero,
. When a is nonzero,
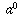 is always defined to be 1, for the reasons given above.
is always defined to be 1, for the reasons given above.
![]() Go backward to Why You Can't Divide Nine By Zero
Go backward to Why You Can't Divide Nine By Zero![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to How To Express A Repeating Decimal Number As A Fraction
Go forward to How To Express A Repeating Decimal Number As A Fraction![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page