(These buttons explained below)
Question Corner and Discussion Area
Who came up with the standard order of operations? When was it originated?I'm going to assume you're referring to the convention that an expression like a + 3 b is understood to mean
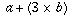and not 
.
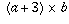This convention is the natural one because multiplication distributes over addition: that is, any product of sums can be re-written as a sum of products (for instance, (2+3)(4) = (2)(4) + (3)(4)), but not every sum of products can be factored as a product of sums.
Therefore, every algebraic expression involving sums and products can always be written as a sum of products. This, then, is the most common, convenient, and natural form in which to write things. Consequently, it makes sense for this to be the form we assume when we omit parentheses in an expression involving sums and products.
That is the origin for the convention that multiplication (and division) have "higher precedence" than addition and subtraction. I do not imagine it originated with any specific person, but was the natural outcome of people wanting to be able to write expressions that were not cluttered with parentheses everywhere, and choosing to interpret such un-parenthesized expressions in the form that is the most universally applicable to all expressions: as a sum of products (for instance, the "3 + (4 times 5)" interpretation of "3 + 4 times 5") rather than as a product of sums (the "(3 + 4) times 5" interpretation), a form which occurs only in factorizable expressions.
Go backward to The Origin Of Geometry Go up to Question Corner Index Go forward to How To Code Information With Error Detection Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page