(These buttons explained below)
Question Corner and Discussion Area
Is there a function f from N (the set of natural numbers) to itself, such that such thatYes, there is such a function. All such functions arise through the following type of construction:(the composition of f with f) sends every n to
?
Let C denote the set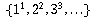 
.
Subdivide the rest of the natural numbers (those that are
not in C) into two disjoint sets
A and B, in any way you like, except that you need to have
infinitely many numbers in each of the two sets.
(For example, you could list the numbers that are not in C:
2,3,5,6,7,. . . . Then let the set A consist of the first number in
this list, the third number in this list, and so on, while B consists
of the second number in this list, the fourth number in this list, and so
on).
Enumerate the numbers in A, calling 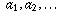them 
.
Similarly, enumerate the numbers in B, calling them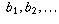 
.
Now define f on the sets A and B by defining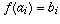 
and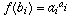 
. (Note that f maps A to B and maps
B to C).
Define f on the set C by setting f(1)=1 and, for all n>1,
define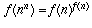 
.
If n is in A or B, this definition is well-defined, for
we have already defined f(n), and the above formula tells us how
to define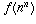 
.
If n is in C, the way we make this definition
correct is to think of it as an inductive definition: assume we have
already defined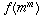 
for all m < n and are now trying to
define 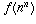. In the case in which n happens to be in C, that
means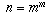 
and it is easy to verify that m < n, hence
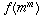has already been defined, and we get an inductive definition
of 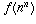in terms of it.
The function f has now been defined for all natural numbers. It remains
to show that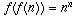 
for all n.
There are three cases.
Case 1: n is in A. Then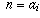 
for some i.
We then have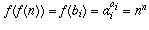 
as required.
Case 2: n is in B. Then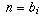 
for some i.
We then have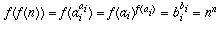 
as required.
Case 3: To prove that
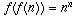for all n in C, suppose to the contrary that there
are some n in C for which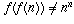 
. Let n=N be the
smallest of these. We know N>1, since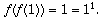 
We also know N is in C, so 
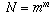for some m,
and clearly m < N (the only time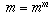 
is when m=1, and
we know that our number N is greater then 1).
Either m is in A, or it is in B, or it is in C but is smaller than
N, and in all three of these cases we already know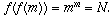 
It follows that 
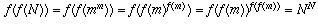. This contradicts our choice of N as being the smallest
counterexample to 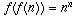, showing that no counterexample
exists,
and hence f has the desired property.
You can also prove that all functions with this property
are given by a construction of the above form.
Assume we have such a function f. The first thing to note is
that f must satisfy the property 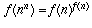for all n,
since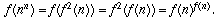 
Now, let C be the same set as above, and divide the numbers that are not in C into two classes, A and B, where A is the set of x not in C for which f(x) is not in C, and B is the set of x not in C for which f(x) is in C.
One can prove that f sets up a one-one correspondence from A to B, as
follows: if x is in A, we know f(x) is not in C, but
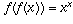which is in C, proving that f(x) is in B.
This proves that f maps A into B.
This mapping is one-to-one: if f(x)=f(y), then f(f(x))=f(f(y)),
so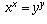 
, and it's easy to verify that for natural numbers
this only happens when x=y.
This mapping is onto: every element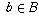 
is obtained as f(a)
for some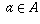 
. This is because
f(b) is in C, so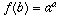 
for some a, and 
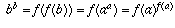from which it follows that b=f(a).
So, if you label the elements of A as 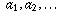and define
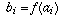, then f is precisely the function defined above,
since 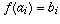(by definition), 
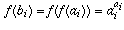(by the argument of the previous paragraph), and for every element
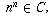
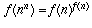. This is precisely the
definition given above.
Go backward to Solving a Quadratic with Non-Constant Coefficients Go up to Question Corner Index Go forward to Largest Possible Number? Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page