(These buttons explained below)
Question Corner and Discussion Area
Howdy folks!That's not an easy question to answer! Mathematically modelling the flow of sound in an enclosed 3-dimensional space requires some advanced techniques in the field of "partial differential equations", and many of the solutions require numerical approximation techniques to actually come up with numerical answers, since many of the functions involved can't be expressed in terms of familiar, everyday functions like addition, multiplication, exponentiation, trigometric functions, etc.I have a question for all you math wizards out there! I make african drums called Ashiko's as a hobby. Until now I have just been guessing the bottom hole size and coming up with some pretty good sounds. . . but I know I could perfect the tone quality if I just knew how to calculate the correct hole size in relation to the top hole and the length. It would sorta be like calculating the port size for a speaker box in a system with a totally enclosed speaker.
For instance. One very popular drum I make is a 12" Ashiko. It has a 12" diameter top hole and a 6" diameter bottom hole with a length of 24". The Ashiko is shaped like a hiway pylon. I stretch a thin, goatskin head over the top hole and lash it tight with 4mm mountain climbing accessory rope.
Any ideas?
River Man
The 1-dimensional situation (e.g., a guitar string, or a thin pipe) is quite easy to analyze. Think about a wave of sound stretched out along the string or pipe, starting with zero amplitude at the end, and rising and falling as you move along the pipe. The amplitude has to be back at zero at the other end (for instance, in a vibrating string, the ends are tied down and not free to move).
Over the course of one cycle (one wavelength),
the displacement of the string (or the compression of air in a pipe)
starts at zero, rises to a positive value, drops back down through zero
to a negative value, then rises again. So the only places at which it is
zero are at the start and end of cycles, and half-way through. In other
words, it is zero at the starting end of the pipe or string, and at a
half-wavelength distance from the end, and at a full wavelength distance
from the end, and at a three-halves-wavelength distance, and so on:
at distances which are an integral multiple of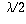 
where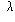 
is the wavelength.
In order for sound to resonate in the string or pipe, the displacement
must be zero at the finishing end as well as the starting end, so the
length L of the pipe must be an integral multiple of .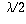
Thus, the only wavelengths that will resonate are when
, 
,
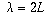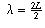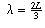, etc.
Frequency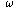 
is related to the wavelength by
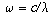where c is the speed of sound.
Therefore, the resonant frequencies are
c/(2L), (2c)/(2L), (3c)/(2L), and so on; in other words, the
fundamental frequency of the string or pipe is c/(2L); the others
are higher octaves. The speed c of sound in a pipe
depends on the air density, humidity,
temperature, altitude, etc. In a string it depends on the string material
and, most importantly, on the string's tension; that's why changing
the tension changes the frequency of sound produced.
However, none of this simple analysis applies to your case, where you are dealing with sound waves in three dimensions. I do not know of any easy answer to your question. I will, however, make sure that your question is seen by others at the University; someone who works in applied mathematics and partial differential equations, or in acoustically related engineering, may be able to offer some insight.
Probably the best thing for you to do is to hunt down a book on the construction of such drums; it would likely contain the measurements for an optimal sound. However, you should realize that those measurements (while as accurate in practice as any computer's computation) were likely obtained by good old fashioned trial and error! In truth, these sorts of measurements are always better than those a computer gives you because there are always many overlooked discrepancies between the mathematical model of the drum and the actual drum (every piece of wood is different, as is every piece of goatskin).
While the modelling process is fascinating in its own right, trial and error (or even better someone else's trial and error) may well be the best route in this particular case.
Go backward to Musical Frequencies and Other Questions Go up to Question Corner Index Go forward to Multiplying Matrices Switch to text-only version (no graphics) Access printed version in PostScript format (requires PostScript printer) Go to University of Toronto Mathematics Network
Home Page