Navigation Panel: 










 Go backward to All People in Canada are the Same Age
Go backward to All People in Canada are the Same Age
 Go up to Classic Fallacies index
Go up to Classic Fallacies index
 Go down to first subsection This is Not the Fallacy
Go down to first subsection This is Not the Fallacy
 Go forward to Every Natural Number can be Unambiguously
Described in Fourteen Words or Less
Go forward to Every Natural Number can be Unambiguously
Described in Fourteen Words or Less
 Switch to text-only version (no graphics)
Switch to text-only version (no graphics)
 Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page
A Ladder Will Fall Infinitely Fast when Pulled
Consider a ladder of length L leaning against a frictionless wall
which is at right angles to the ground.
You pull the bottom of the ladder horizontally away from the wall, at
constant speed v. The claim is that this causes the top of the
ladder to fall infinitely fast.
Common sense tells us this can't possibly be true, but can you find
the flaw in the following supposed "proof" of this claim?

The Fallacious Proof:
-
Step 1: As shown, let x denote the
horizontal distance from the bottom of the
ladder to the wall, at time t.
-
Step 2: As shown, let y denote the height
of the top of the ladder from the ground, at
time t.
-
Step 3: Since the ladder, the ground, and the wall form
a right triangle,
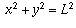 .
.
-
Step 4: Therefore,
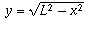 .
.
-
Step 5: Differentiating, and letting
x' and y' (respectively) denote the
derivatives of x and y with respect to t,
we get that
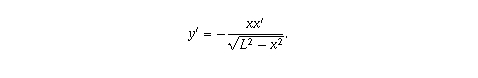
-
Step 6: Since the bottom of the ladder is being
pulled with constant speed v, we have x' = v,
and therefore
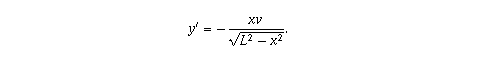
-
Step 7: As x approaches L,
the numerator in this expression for y' approaches
-Lv which is nonzero, while the denominator
approaches zero.
-
Step 8: Therefore, y' approaches
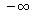 as x approaches L. In other words,
the top of the ladder is falling infinitely fast by the time
the bottom has been pulled a distance L away from the wall.
as x approaches L. In other words,
the top of the ladder is falling infinitely fast by the time
the bottom has been pulled a distance L away from the wall.
See if you can figure out in which step the fallacy lies.
When you think you've figured it out, click on that step and
the computer will tell you whether you are correct or not, and
will give an additional explanation of why that step is or isn't valid.
See how many tries it takes you to correctly identify the fallacious step!
This page last updated: May 26, 1998
Original Web Site Creator / Mathematical Content Developer:
Philip Spencer
Current Network Coordinator and Contact Person:
Joel Chan - mathnet@math.toronto.edu
Navigation Panel: 












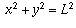 .
.
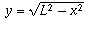 .
.
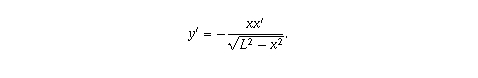
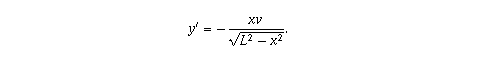
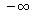 as x approaches L. In other words,
the top of the ladder is falling infinitely fast by the time
the bottom has been pulled a distance L away from the wall.
as x approaches L. In other words,
the top of the ladder is falling infinitely fast by the time
the bottom has been pulled a distance L away from the wall.